题目内容
3．
如图，在?ABCD中，AE⊥BD于点E，∠EAC=30°，AC=12，则AE的长为3$\sqrt{3}$．
分析 由在?ABCD中，AC=12，根据平行四边形对角线互相平分，可求得OA的长，然后由AE⊥BD，∠EAC=30°，利用三角函数的知识，求得答案．
解答 解：∵在?ABCD中，AC=12，
∴OA=$\frac{1}{2}$AC=6，
∵AE⊥BD，∠EAC=30°，
∴AE=OA•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$．
故答案为：3$\sqrt{3}$．
点评 此题考查了平行四边形的性质以及特殊角的三角函数值．注意平行四边形的对角线互相平分．
练习册系列答案
阅读快车系列答案
相关题目
14．矩形具有而一般平行四边形不具有的特征是（ ）
| A． | 对边相等 | B． | 对角相等 | C． | 对角线相等 | D． | 对角线互相平分 |
11．已知点P（2-a，3a+6）到两坐标轴的距离相等，则点P的坐标为（ ）
| A． | （3，3）或（6，-6） | B． | （3，-3）或 （6，-6） | C． | （3，3） | D． | （3，-3） |
18．
如图，在矩形ABCD中，AD=3，AB＞3，AG平分∠BAD，分别过点B、C作BE⊥AG于点E，CF⊥AG于点F，则（AE-GF）的值为（ ）
如图，在矩形ABCD中，AD=3，AB＞3，AG平分∠BAD，分别过点B、C作BE⊥AG于点E，CF⊥AG于点F，则（AE-GF）的值为（ ）| A． | 3 | B． | $\frac{{3\sqrt{2}}}{2}$ | C． | $\frac{{3\sqrt{3}}}{2}$ | D． | $3\sqrt{2}$ |
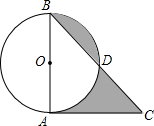如图，AB是⊙O的直径，BD是弦，过点A的切线交BD延长线于点C．若AB=AC=4，则图中阴影部分图形的面积和是4．
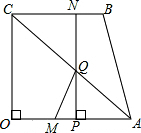如图，四边形OABC为直角梯形，OA∥BC，∠AOC=90°，OA=OC=4，BC=3．点M从O出发以每秒2个单位长度的速度向A运动；点N从B同时出发，以每秒1个单位长度的速度向C运动，当其中一个动点达到终点时，另一个动点也随之停止运动，过点N作NP垂直OA于点P，连接AC交NP于点Q，连接MQ．
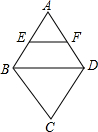如图，在菱形ABCD中，∠BAD=60°，点E、F分别是AB、AD的中点，若S△AEF=4，则S五边形EBCDF=28．
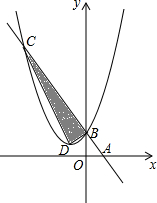如图，在直角坐标系中，点A，B的坐标分别为（1，0），（0，2），某抛物线的顶点坐标为D（-1，1）且经过点B，连接AB，直线AB与抛物线相交于点C，则S△ABO：S△BCD=（ ）