题目内容
13.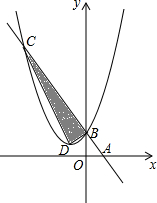 如图,在直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与抛物线相交于点C,则S△ABO:S△BCD=( )
如图,在直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与抛物线相交于点C,则S△ABO:S△BCD=( )| A. | 1:8 | B. | 1:6 | C. | 1:4 | D. | 1:3 |
分析 设直线AB的解析式为y=kx+b,二次函数的解析式为y=a(x+1)2+1,结合点的坐标利用待定系数法求出一次函数与二次函数的解析式,联立一次函数与二次函数解析式解出交点C的坐标,根据两点间的距离公式求出线段BC、AB的长度,再借用点到直线的距离公式寻找到点D、O到直线AB的距离间的关系,利用三角形的面积公式即可得出结论.
解答 解:设直线AB的解析式为y=kx+b,二次函数的解析式为y=a(x+1)2+1,
将点A(1,0)、B(0,2)代入y=kx+b中得:$\left\{\begin{array}{l}{k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-2x+2,
将点B(0,2)代入到y=a(x+1)2+1中得,
2=a+1,
解得:a=1,
∴二次函数的解析式为y=(x+1)2+1=x2+2x+2.
将y=-2x+2代入y=x2+2x+2中得,
-2x+2=x2+2x+2,
整理得:x2+4x=0,
解得:x1=-4,x2=0,
∴点C的坐标为(-4,10).
∵点C(-4,10),点B(0,2),点A(1,0),
∴AB=$\sqrt{5}$,BC=4$\sqrt{5}$,
∴BC=4AB.
∵直线AB解析式为y=-2x+2可变形为2x+y-2=0,
∴|-2+1-2|=3,|-2|=2.
∴S△ABO:S△BCD=2:12=1:6.
故选:B.
点评 本题考查了二次函数的性质、两点间的距离公式、点到直线的距离公式以及三角形的面积公式,解决该题型题目时,结合点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.


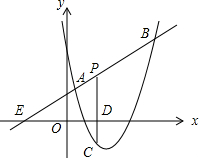 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C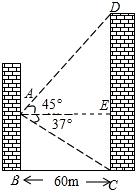 如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)