题目内容
18. 如图,在矩形ABCD中,AD=3,AB>3,AG平分∠BAD,分别过点B、C作BE⊥AG于点E,CF⊥AG于点F,则(AE-GF)的值为( )
如图,在矩形ABCD中,AD=3,AB>3,AG平分∠BAD,分别过点B、C作BE⊥AG于点E,CF⊥AG于点F,则(AE-GF)的值为( )| A. | 3 | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $3\sqrt{2}$ |
分析 设AE=x,则AB=$\sqrt{2}$x,由矩形的性质得出∠BAD=∠D=90°,CD=AB,证明△ADG是等腰直角三角形,得出AG=$\sqrt{2}$AD=3$\sqrt{2}$,同理得出CD=AB=$\sqrt{2}$x,CG=CD-DG,得出GF,即可得出结果.
解答 解:设AE=x,
∵四边形ABCD是矩形,
∴∠BAD=∠D=90°,CD=AB,
∵AG平分∠BAD,∴∠DAG=45°,
∴△ADG是等腰直角三角形,
∴DG=AD=3,
∴AG=$\sqrt{2}$AD=3$\sqrt{2}$,
同理:BE=AE=x,CD=AB=$\sqrt{2}$x,
∴CG=CD-DG=$\sqrt{2}$x-3,
同理:CG=$\sqrt{2}$FG,
∴FG=$\frac{\sqrt{2}}{2}$CG=x-$\frac{3\sqrt{2}}{2}$,
∴AE-GF=x-(x-$\frac{3\sqrt{2}}{2}$)=$\frac{3\sqrt{2}}{2}$.
故选:B.
点评 本题考查了矩形的性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质和等腰直角三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若点P是线段MN的中点,则下列结论不正确的是( )
| A. | MP=NP | B. | MN=2NP | C. | MP=$\frac{1}{2}$MN | D. | MN=$\frac{1}{2}$NP |
10.一条开口向下的抛物线的顶点坐标是(2,3),则这条抛物线有( )
| A. | 最大值3 | B. | 最小值3 | C. | 最大值2 | D. | 最小值-2 |
 如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.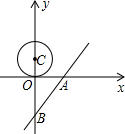 在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.