题目内容
12.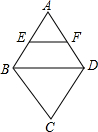 如图,在菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD的中点,若S△AEF=4,则S五边形EBCDF=28.
如图,在菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD的中点,若S△AEF=4,则S五边形EBCDF=28.
分析 根据三角形的中位线性质得出EF=$\frac{1}{2}$BD,EF∥BD,根据相似三角形的判定得出△ABD∽△AEF,根据相似三角形的性质求出S△ABD=4S△AEF=16,求出S△ABD=S△BCD=16,代入S五边形EBCDF=S△ABD+S△BCD-S△AEF求出即可.
解答 解:∵E,F分别是AB,AD的中点,
∴EF=$\frac{1}{2}$BD,EF∥BD,
∴△ABD∽△AEF,
∴S△ABD=4S△AEF=16,
又∵在菱形ABCD中,∠BAD=60°,
∴S△ABD=S△BCD,
∴S五边形EBCDF=S△ABD+S△BCD-S△AEF=16+16-4=28.
点评 本题考查了菱形的性质,三角形的中位线性质,相似三角形的性质和判定的应用,能灵活运用性质进行推理和计算是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.

练习册系列答案
相关题目
17.厦门市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月进行了公共日租车量的统计,估计4月份共租车2500000次,2500000用科学记数法表示为( )
| A. | 25×105 | B. | 2.5×106 | C. | 0.25×107 | D. | 2.5×107 |
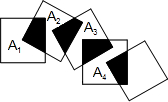 将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为4.
将五个边长都为2的正方形按如图所示摆放,点A1、A2、A3、A4分别是四个正方形的中心,则图中四块阴影部分的面积的和为4. 如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.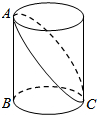 如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.
如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.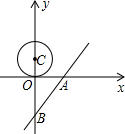 在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.