题目内容
8.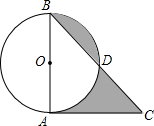 如图,AB是⊙O的直径,BD是弦,过点A的切线交BD延长线于点C.若AB=AC=4,则图中阴影部分图形的面积和是4.
如图,AB是⊙O的直径,BD是弦,过点A的切线交BD延长线于点C.若AB=AC=4,则图中阴影部分图形的面积和是4.
分析 连接OD,根据圆周角定理求出∠AOD的度数,再由S阴影=(S△ABC-S扇形AOD-S△BOD)+(S扇形BOD-S△BOD)即可得出结论.
解答 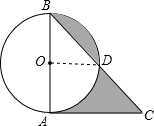 解:连接OD,
解:连接OD,
∵AB为⊙O的直径,AC为切线,AB=AC=4,
∴∠BAC=90°,OA=OB=2,∠ABC=45°,
∴∠AOD=90°,△BOD是等腰直角三角形,
∴S阴影=(S△ABC-S扇形AOD-S△BOD)+(S扇形BOD-S△BOD)=($\frac{1}{2}$×4×4-$\frac{90π×4}{360}$-$\frac{1}{2}$×2×2)+($\frac{90π{2}^{2}}{360}$-$\frac{1}{2}$×2×2)
=8-π-2+(π-2)
=6-π+π-2
=4.
故答案为:4.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
13.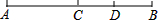 如图,C是线段AB的中点,D是线段CB的中点,下列说法错误的是( )
如图,C是线段AB的中点,D是线段CB的中点,下列说法错误的是( )
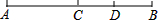 如图,C是线段AB的中点,D是线段CB的中点,下列说法错误的是( )
如图,C是线段AB的中点,D是线段CB的中点,下列说法错误的是( )| A. | CD=AC-BD | B. | CD=$\frac{1}{2}$AB-BD | C. | AC+BD=BC+CD | D. | CD=$\frac{1}{3}$AB |
17.厦门市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月进行了公共日租车量的统计,估计4月份共租车2500000次,2500000用科学记数法表示为( )
| A. | 25×105 | B. | 2.5×106 | C. | 0.25×107 | D. | 2.5×107 |
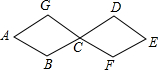 两个全等菱形如图所示摆放在一起,其中B、C、D和G、C、F分别在同一条直线上,若较短的对角线长为10,点G与点D的距离是24,则此菱形边长为13.
两个全等菱形如图所示摆放在一起,其中B、C、D和G、C、F分别在同一条直线上,若较短的对角线长为10,点G与点D的距离是24,则此菱形边长为13.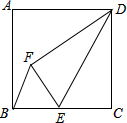 如图,在边长为12的正方形ABCD中,点E是边BC的中点,将△DCE沿DE折叠,点C落在正方形内的点F处,则△BEF的面积为$\frac{72}{5}$.
如图,在边长为12的正方形ABCD中,点E是边BC的中点,将△DCE沿DE折叠,点C落在正方形内的点F处,则△BEF的面积为$\frac{72}{5}$. 如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.
如图,在?ABCD中,AE⊥BD于点E,∠EAC=30°,AC=12,则AE的长为3$\sqrt{3}$.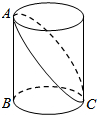 如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.
如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为4$\sqrt{2}$dm.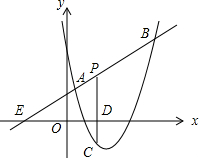 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( $\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C