Question

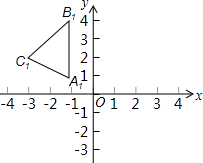已知△A₁B₁C₁是由△ABC向上平移1个单位长度，向左平移3个单位长度得到的，且A₁（-1，1），B₁（-1，4），C₁（-3，2）．
（1）在直角坐标系内画出△ABC并写出A、B、C三点的坐标；
（2）求△ABC的面积；
（3）若点P（m，

1

2

）是坐标平面内一点，是否存在这样的数m，使△ACP的面积与△ABC的面积相等？若存在，求出m的值；若不存在，说明理由．

Answer 1

考点：作图-平移变换

专题：

分析：（1）利用平移规律进而得出对应点坐标；
（2）利用各点坐标得出图形的面积；
（3）利用三角形面积求法得出

1

2

（m-1）×

1

2

+

1

2

（m-1）×

1

2

=3或

1

2

（-1-m）×

1

2

+

1

2

（-1-m）×

1

2

=3进而得出答案．

解答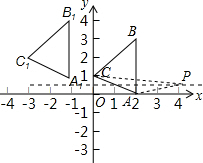：解：（1）如图所示：△ABC即为所求；
A（2，0）、B（2，3）、C（0，1）；

（2）△ABC的面积为：

1

2

×2×3=3；

（3）存在，
理由：由题意可得：当△ACP的面积与△ABC的面积相等，
则

1

2

（m-1）×

1

2

+

1

2

（m-1）×

1

2

=3或

1

2

（-1-m）×

1

2

+

1

2

（-1-m）×

1

2

=3，
解得：m=7或-5．

点评：此题主要考查了平移变换以及三角形面积求法，利用数形结合得出是解题关键．