题目内容
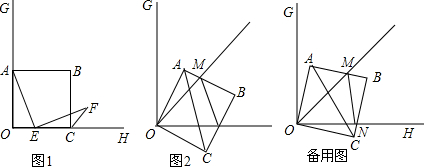
已知∠GOH=90°,A、C分别是OG、OH上的点,且OA=OC=4,以OA为边长作正方形OABC.
(1)E是边OC上一点,作∠AEF=90°使EF交正方形的外角平分线CF于点F(如图1),求证:EF=AE.
(2)现将正方形OABC绕O点顺时针旋转,当A点第一次落在∠GOH的角平分线OP上时停止旋转;旋转过程中,AB边交OP于点M,BC边交OH于点N(如图2),
①旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
②设△MBN的周长为p,在正方形OABC的旋转过程中,p值是否有变化?请证明你的结论.
(1)E是边OC上一点,作∠AEF=90°使EF交正方形的外角平分线CF于点F(如图1),求证:EF=AE.
(2)现将正方形OABC绕O点顺时针旋转,当A点第一次落在∠GOH的角平分线OP上时停止旋转;旋转过程中,AB边交OP于点M,BC边交OH于点N(如图2),
①旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
②设△MBN的周长为p,在正方形OABC的旋转过程中,p值是否有变化?请证明你的结论.

考点:几何变换综合题
专题:
分析:(1)如图1,作辅助线,证明△AME≌△ECF,即可解决问题.
(2)如图2,根据题意结合图形,证明△OAM≌△OCN,得到∠AOM=∠CON=
=22.5°,求出∠GOA即可解决问题.
(3)如图3,作辅助线,证明△OAM≌△OCQ,得到OM=OQ,∠MON=∠QON;证明△OMN≌△OQN,得到MN=QN=AM+CN,问题即可解决.
(2)如图2,根据题意结合图形,证明△OAM≌△OCN,得到∠AOM=∠CON=
| 90°-45° |
| 2 |
(3)如图3,作辅助线,证明△OAM≌△OCQ,得到OM=OQ,∠MON=∠QON;证明△OMN≌△OQN,得到MN=QN=AM+CN,问题即可解决.
解答: 解:(1)如图1,
解:(1)如图1,
在OA上截取线段AM,使AM=CE;
∵四边形ABCO是正方形,
∴AO=CO,∠O=∠ECB=90°;
∴OM=OE,∠OME=45°;而OF平分∠BCH,
∴∠AME=135°,∠ECF=90°+45°=135°;
∵AE⊥EF,∠O=90°,
∴∠OAE+∠AEO=∠AEO+∠CEF,
∴∠OAE=∠CEF;
在△AME与△ECF中,
,
∴△AME≌△ECF(ASA),
∴EF=AE.
 (2)如图2,∵MN∥AC,
(2)如图2,∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,BM=BN;
∵AB=BC,
∴AM=CN;
∵四边形ABCO是正方形,
∴AO=CO,∠OAM=∠OCN;
在△OAM与△OCN中,
,
∴△OAM≌△OCN(SAS),
∴∠AOM=∠CON=
=22.5°,
∴∠GOA=45°-22.5°=22.5°,
即当MN和AC平行时,正方形OABC旋转了22.5°.
 (3)如图3,延长BC到Q,使CQ=AM,连接OQ;
(3)如图3,延长BC到Q,使CQ=AM,连接OQ;
在△OAM与△OCQ中,
,
∴△OAM≌△OCQ(SAS),
∴∠COQ=∠AOM,
∠QON=∠AOM+∠CON=45°,
OM=OQ;
在△OMN与△OQN中,
,
∴△OMN≌△OQN(SAS),
∴MN=QN=AM+CN,
∴△MBN的周长p=2AB=8,为定值,不变.
 解:(1)如图1,
解:(1)如图1,在OA上截取线段AM,使AM=CE;
∵四边形ABCO是正方形,
∴AO=CO,∠O=∠ECB=90°;
∴OM=OE,∠OME=45°;而OF平分∠BCH,
∴∠AME=135°,∠ECF=90°+45°=135°;
∵AE⊥EF,∠O=90°,
∴∠OAE+∠AEO=∠AEO+∠CEF,
∴∠OAE=∠CEF;
在△AME与△ECF中,
|
∴△AME≌△ECF(ASA),
∴EF=AE.
 (2)如图2,∵MN∥AC,
(2)如图2,∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM,BM=BN;
∵AB=BC,
∴AM=CN;
∵四边形ABCO是正方形,
∴AO=CO,∠OAM=∠OCN;
在△OAM与△OCN中,
|
∴△OAM≌△OCN(SAS),
∴∠AOM=∠CON=
| 90°-45° |
| 2 |
∴∠GOA=45°-22.5°=22.5°,
即当MN和AC平行时,正方形OABC旋转了22.5°.
 (3)如图3,延长BC到Q,使CQ=AM,连接OQ;
(3)如图3,延长BC到Q,使CQ=AM,连接OQ;在△OAM与△OCQ中,
|
∴△OAM≌△OCQ(SAS),
∴∠COQ=∠AOM,
∠QON=∠AOM+∠CON=45°,
OM=OQ;
在△OMN与△OQN中,
|
∴△OMN≌△OQN(SAS),
∴MN=QN=AM+CN,
∴△MBN的周长p=2AB=8,为定值,不变.
点评:该题以正方形为载体,以旋转变换为方法,以全等三角形的判定及其性质、正方形的性质等重要几何知识点为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
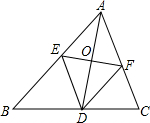 如图所示,△ABC中,D为BC上一个点,EF垂直平分AD交AB于E,交AC于F,若DE∥AC,判断四边形AEDF的形状并说明理由.
如图所示,△ABC中,D为BC上一个点,EF垂直平分AD交AB于E,交AC于F,若DE∥AC,判断四边形AEDF的形状并说明理由.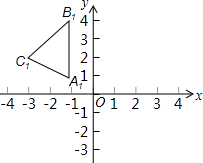 已知△A1B1C1是由△ABC向上平移1个单位长度,向左平移3个单位长度得到的,且A1(-1,1),B1(-1,4),C1(-3,2).
已知△A1B1C1是由△ABC向上平移1个单位长度,向左平移3个单位长度得到的,且A1(-1,1),B1(-1,4),C1(-3,2). 在4×4的正方形中,以格点与格点为端点,你能画出几条边长为整数的线段(不包括长度为1,2,3,4的线段).
在4×4的正方形中,以格点与格点为端点,你能画出几条边长为整数的线段(不包括长度为1,2,3,4的线段). 如图,E为等边△ABC的边AC上一点,且∠1=∠2,CD=BE,试判定△ADE的形状,并说明理由.
如图,E为等边△ABC的边AC上一点,且∠1=∠2,CD=BE,试判定△ADE的形状,并说明理由.