题目内容
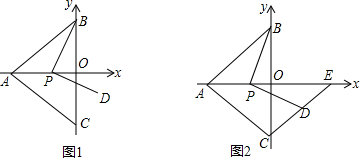
如图1,在平面直角坐标系中,已知A(-5,0),C(0,-4),点B在y轴正半轴上,满足S△ABC=20,点P(m,0),(-4<m<0),线段PB绕点P顺时针旋转90°至PD.
(1)求证:OB=OC;
(2)求点D的坐标;(用含m的式子表示)
(3)如图2,连接CD并延长交x轴于点E,求证:∠PDC=45°+∠PBO.
(1)求证:OB=OC;
(2)求点D的坐标;(用含m的式子表示)
(3)如图2,连接CD并延长交x轴于点E,求证:∠PDC=45°+∠PBO.

考点:全等三角形的判定与性质,坐标与图形性质,三角形的面积
专题:
分析:(1)根据△BAC面积即可求得BC的长,即可解题;
(2)作DF⊥AE,易证∠PBO=∠DPF,即可证明△OPB≌△FDP,可得DF=OP,PF=OB,即可求得点D坐标;
(3)易求直线CD斜率即可求得∠DEF的大小,根据△OPB≌△FDP可得∠PBO=∠DPF,根据三角形外角性质即可解题.
(2)作DF⊥AE,易证∠PBO=∠DPF,即可证明△OPB≌△FDP,可得DF=OP,PF=OB,即可求得点D坐标;
(3)易求直线CD斜率即可求得∠DEF的大小,根据△OPB≌△FDP可得∠PBO=∠DPF,根据三角形外角性质即可解题.
解答:(1)证明:∵S△ABC=20,
∴
BC•AO=20,
∴BC=8,
∵CO=4,∴BO=4,
∴B点坐标(0,4);
(2)解:作DF⊥AE,
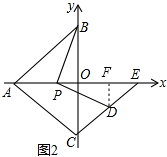
∵∠PBO+∠OPB=90°,∠OPB+∠DPF=90°,
∴∠PBO=∠DPF,
∵在△OPB和△FDP中,
,
∴△OPB≌△FDP,(AAS)
∴DF=OP=-m,PF=OB=4,
∴点D坐标(4+m,m);
(3)证明:∵直线CD经过C,D两点,
∴直线CD斜率为
=1,
∴∠DEF=45°,
∵△OPB≌△FDP,
∴∠PBO=∠DPF,
∵∠CDP=∠DPF+∠DEF,
∴∠CDP=∠PBO+45°.
∴
| 1 |
| 2 |
∴BC=8,
∵CO=4,∴BO=4,
∴B点坐标(0,4);
(2)解:作DF⊥AE,

∵∠PBO+∠OPB=90°,∠OPB+∠DPF=90°,
∴∠PBO=∠DPF,
∵在△OPB和△FDP中,
|
∴△OPB≌△FDP,(AAS)
∴DF=OP=-m,PF=OB=4,
∴点D坐标(4+m,m);
(3)证明:∵直线CD经过C,D两点,
∴直线CD斜率为
| m-(-4) |
| m+4-0 |
∴∠DEF=45°,
∵△OPB≌△FDP,
∴∠PBO=∠DPF,
∵∠CDP=∠DPF+∠DEF,
∴∠CDP=∠PBO+45°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△OPB≌△FDP是解题的关键.

练习册系列答案
相关题目
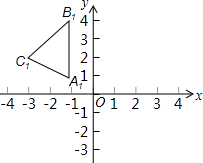 已知△A1B1C1是由△ABC向上平移1个单位长度,向左平移3个单位长度得到的,且A1(-1,1),B1(-1,4),C1(-3,2).
已知△A1B1C1是由△ABC向上平移1个单位长度,向左平移3个单位长度得到的,且A1(-1,1),B1(-1,4),C1(-3,2).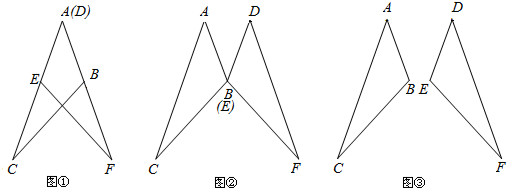
 如图,AB=DE,AC=DF,BE=CF,且B,E,C,F在同一条直线上,若∠EGC=80°,求∠A的度数.
如图,AB=DE,AC=DF,BE=CF,且B,E,C,F在同一条直线上,若∠EGC=80°,求∠A的度数.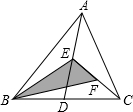 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为
如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE中点,且S△ABC=4平方厘米,则S△BEF的值为