题目内容
6.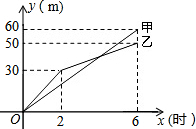 有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:
有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:①施工6小时,甲队比乙队多施工了10米;
②施工4小时,甲、乙两队施工的长度相同;
③施工5小时,甲乙两队共完成路面铺设任务95米;
④如果甲队在施工6小时后继续保持原来施工速度,且又经过5个小时完成铺设任务,乙队在施工50米后,恢复其前30米时的施工速度,结果两队同时完成了铺设任务,
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图中的信息可从中找到甲、乙两队各组数据,并且利用待定系数法即可确定函数关系式进行判断即可.
解答 解:①施工6小时,甲队比乙队多施工了60-50=10米,正确;
设甲队在0≤x≤6的时段内y与x之间的函数关系式y=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y=10x,
设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=k2x+b,
由图可知,函数图象过点(2,30)、(6,50),
∴$\left\{\begin{array}{l}{2{k}_{2}+b=30}\\{6{k}_{2}+b=50}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=5}\\{b=20}\end{array}\right.$,
∴y=5x+20,
②由题意,得10x=5x+20,
解得x=4.
∴当x为4h时,甲、乙两队所挖的河渠长度相等,正确;
③把x=5代入解析式y=10x=50,
把x=5代入解析式y=5x+20=45,
45+50=95,施工5小时,甲乙两队共完成路面铺设任务95米,正确;
④由题意可得:甲一共施工11小时,则路面总长度为:110m,
∵乙队在施工50米,需要6小时,还剩余60m,则还需要:60÷(30÷2)=4(小时),
故乙队施工10小时,则结果两队不能同时完成铺设任务,故此选项错误.
故选:C.
点评 此题主要考查学生对函数图象掌握情况及利用待定系数法求一次函数关系式,理解题意是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.八年级的同学们即将步入初三,某主题班会小组为了了解本校八年级同学对初三的第一印象,打算抽样调查40位同学.
(1)有同学提议:“八年级1班的人数刚好是40人,不如我们直接调查1班所有同学吧”,他的建议合理吗?请说明理由;
(2)他们用问卷随机调查了40位同学(每人只能选一项),并统计如下:
请选择一种统计图将上表中的数据描述出来;
(3)若本校八年级共有500名学生,请估计对初三第一印象是“忧喜交加”的同学人数.
(1)有同学提议:“八年级1班的人数刚好是40人,不如我们直接调查1班所有同学吧”,他的建议合理吗?请说明理由;
(2)他们用问卷随机调查了40位同学(每人只能选一项),并统计如下:
| 第一印象 | 满怀期待 | 忧喜交加 | 想想都累 | 放过我吧 | 其他 |
| 划记 | 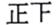 | 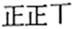 |  | 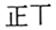 |  |
(3)若本校八年级共有500名学生,请估计对初三第一印象是“忧喜交加”的同学人数.
3.若二次根式$\sqrt{2-x}$有意义,则x的取值范围是( )
| A. | x<2 | B. | x≠2 | C. | x≤2 | D. | x≥2 |
20. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )| A. | 47m | B. | 51m | C. | 53m | D. | 54m |
18.方程2x+y=9在正整数范围内的解有( )
| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
16.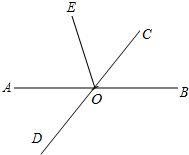 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
 如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )
如图,已知直线AB与CD相交于点O,OC平分∠BOE,若∠AOE=80°,则∠AOD的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |

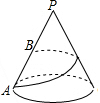 已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)
已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)