题目内容
20. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )
济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,$\sqrt{3}$≈1.7,结果精确到1m,则该楼的高度CD为( )| A. | 47m | B. | 51m | C. | 53m | D. | 54m |
分析 由题意易得:∠A=30°,∠DBC=60°,DC⊥AC,即可证得△ABD是等腰三角形,然后利用三角函数,求得答案.
解答 解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC-∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=60m,
∴CD=BD•sin60°=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$≈51(m).
故选B.
点评 此题考查了解直角三角形的应用-仰角俯角问题.注意证得△ABD是等腰三角形,利用特殊角的三角函数值求解是关键.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=4 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | (-$\sqrt{2}$)2=2 |
15.下列运算正确的是( )
| A. | 3a+2a=5a2 | B. | x2-4=(x+2)(x-2) | C. | (x+1)2=x2+1 | D. | (2a)3=6a3 |
5.已知代数式$\sqrt{1-x}$+$\sqrt{\frac{1}{x}}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1 | B. | 0<x≤1 | C. | x>0 | D. | 0≤x≤1 |
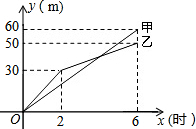 有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:
有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法: