题目内容
已知两弦AB和CD相交于圆内一点P,并且两弦的夹角被经过P点的直径平分.求证:AB=CD.
考点:垂径定理,角平分线的性质,勾股定理
专题:证明题
分析:根据题意画出图形,过O分别做AB,CD的垂线,垂足为E,F,根据角平分线的性质得出OE=OF,由HL定理得出△BOE≌△COF,故可得出BE=CF,由垂径定理即可得出结论.
解答: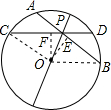 证明:如图所示,过O分别做AB,CD的垂线,垂足为E,F,连接OC,OB,
证明:如图所示,过O分别做AB,CD的垂线,垂足为E,F,连接OC,OB,
∵OP为∠CPB的角平分线,
∴OE=OF.
在Rt△BOE与Rt△COF中,
,
∴△BOE≌△COF(HL),
∴BE=CF.
∵OF⊥CD,OE⊥AB,
∴CD=2CF,AB=2BE,
∴AB=CD.
 证明:如图所示,过O分别做AB,CD的垂线,垂足为E,F,连接OC,OB,
证明:如图所示,过O分别做AB,CD的垂线,垂足为E,F,连接OC,OB,∵OP为∠CPB的角平分线,
∴OE=OF.
在Rt△BOE与Rt△COF中,
|
∴△BOE≌△COF(HL),
∴BE=CF.
∵OF⊥CD,OE⊥AB,
∴CD=2CF,AB=2BE,
∴AB=CD.
点评:本题考查的是垂径定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D为AB中点,CE⊥AB,则∠DCE=
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D为AB中点,CE⊥AB,则∠DCE=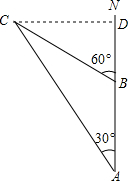 如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?
如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)? 如图,在⊙O中,半径OA=8cm,cos∠A=
如图,在⊙O中,半径OA=8cm,cos∠A=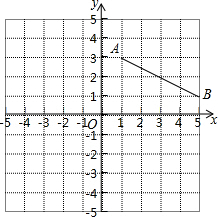 如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( )
如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( ) 如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.
如图,已知A、B、C、D四点在⊙O上,AB、CD交于点E,AD=BC,求证:AB=CD.