题目内容
如图，Rt△ABC中，∠ACB=90°，∠A=35°，D为AB中点，CE⊥AB，则∠DCE=考点：直角三角形斜边上的中线
专题：
分析：根据斜边上的中线等于斜边的一半可求得CD=DA，可求得∠CDE=70°，再根据直角三角形两锐角互余可求得∠DCE．
解答：解：
∵∠ACB=90°，D为AB中点，
∴DC=DA，
∴∠A=∠ACD，
∴∠CDE=2∠A=2×35°=70°，
∵CE⊥AB，
∴∠DCE=90°-∠CDE=90°-70°=20°，
故答案为：20．
∵∠ACB=90°，D为AB中点，
∴DC=DA，
∴∠A=∠ACD，
∴∠CDE=2∠A=2×35°=70°，
∵CE⊥AB，
∴∠DCE=90°-∠CDE=90°-70°=20°，
故答案为：20．
点评：本题主要考查直角三角形的性质，掌握直角三角形中斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
相关题目
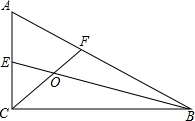如图，∠ACB=90°，∠ABC=30°，BE、CF分别平分∠ABC、∠ACB，交AC、AB于点E、F，BE，CF交于点O，求证：OE=OF．
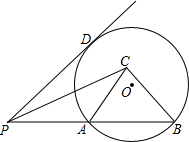如图，PD切⊙O于D，PC=PD，B为⊙O上一点，PB交⊙O于A，连结AC、BC．求证：AC•PB=PC•BC．