题目内容
19.已知二次函数y=x2+bx+3,其中b为常数,当x≥2时,函数值y随着x的增大而增大,则b的取值范围是b≥-4.分析 根据二次函数解析式可找出二次函数的对称轴,再由二次项系数>0即可得出二次函数的单增区间,结合给定条件即可得出关于b的一元一次不等式,解不等式即可得出结论.
解答 解:∵二次函数y=x2+bx+3的对称轴为x=-$\frac{b}{2a}$=-$\frac{b}{2}$,且a=1>0,
∴当x≥-$\frac{b}{2}$时,函数值y随着x的增大而增大,
∵当x≥2时,函数值y随着x的增大而增大,
∴-$\frac{b}{2}$≤2,
解得:b≥-4.
点评 本题考查了二次函数的性质以及解一元一次不等式,解题的关键是根据二次函数的性质找出二次函数的单增区间.本题属于基础题,难度不大,解决该题型题目时,根据二次函数性质找出单增区间,再结合题意得出不等式是关键.

练习册系列答案
相关题目
7. 如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )
如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )
 如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )
如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )| A. | (2,2) | B. | (-2,2) | C. | (-2,-2) | D. | (2,2)或(-2,-2) |
 发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.
发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B、C、E三点共线,且BC:CE=2:1,连接AE、BD.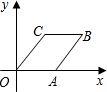 菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B.
菱形OABC在平面直角坐标系中的位置如图所示,点C(3,4),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B. 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿着过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的长等于5π.(结果保留π)
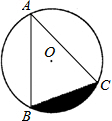 如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π).
如图,点A、B、C在直径为4$\sqrt{3}$的⊙O上,∠BAC=45°,则图中阴影部分的面积等于3π-6(结果保留π). 如图,OC是∠AOB的平分线,且CD∥OA,∠C=26°,则∠AOB的度数等于52°.
如图,OC是∠AOB的平分线,且CD∥OA,∠C=26°,则∠AOB的度数等于52°. 如图,已知圆锥母线长30cm,底面半径r=8cm,则这个圆锥的侧面积是240πcm2.
如图,已知圆锥母线长30cm,底面半径r=8cm,则这个圆锥的侧面积是240πcm2.