Question

16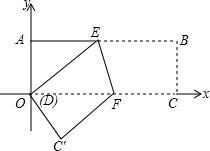．如图，在直角坐标系中，长方形纸片ABCD的边AB∥CO，点B坐标为（9，3），若把图形按如图所示折叠，使B、D两点重合，折痕为EF．
（1）求证：△DEF为等腰三角形；
（2）求折痕EF的长．

Answer 1

分析 （1）由四边形ABCD是矩形，可得AB∥OC，又由折叠的性质可得：∠BEF=∠OEF，即可证得∠OEF=∠OFE，则可得OE=OF；
（2）首先设BE=OE=x，则AE=9-x，可得方程（9-x）²+3²=x²，继而求得点E，F的坐标，即可求得折痕EF的长．

解答 解：（1）∵四边形ABCD是矩形，
∴AB∥OC，
∴∠BEF=∠OFE，
由折叠的性质可得：∠BEF=∠OEF，
∴∠OEF=∠OFE，
∴OE=OF，
∴△OEF是等腰三角形；
（2）设BE=OE=x，则AE=9-x，
在Rt△AEO中，AE²+OA²=OE²，
∴（9-x）²+3²=x²，
解得：x=5，
∴OF=OE=5，AE=4，
∴E（4，3），F（5，0），
∴EF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$．

点评 本题考查了翻折变换的性质，等腰三角形的判定与性质，熟记性质并利用勾股定理列出方程是解题的关键．