题目内容
1.在△ABC中,AB=2cm,AC=1cm,AD平分∠BAC,则△ABD与△ACD的面积之比是2:1.分析 根据角平分线的性质得出DE=DF,根据三角形面积公式求出两三角形面积之比=AB:AC,代入求出即可.
解答 解:如图,过D作DE⊥AB于E,DF⊥AC于F, ∵AD是△ABC的角平分线,
∵AD是△ABC的角平分线,
∴DE=DF,
∵S△ABD=$\frac{1}{2}$×AB×DE,S△ACD=$\frac{1}{2}$×AC×DF,
∴△ABD与△ACD的面积之比为AB:AC=2:1.
故答案为:2:1.
点评 本题考查了角平分线的性质,以及三角形的面积公式,熟练掌握三角形角平分线的性质是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
6.下列方程中,不是二元一次方程的是( )
| A. | x-2y=3 | B. | x=2y | C. | xy=3 | D. | x-y=1+y |
10. 如图,在⊙O中$\widehat{AC}$=$\widehat{BD}$,∠AOB=40°,则∠COD的度数( )
如图,在⊙O中$\widehat{AC}$=$\widehat{BD}$,∠AOB=40°,则∠COD的度数( )
 如图,在⊙O中$\widehat{AC}$=$\widehat{BD}$,∠AOB=40°,则∠COD的度数( )
如图,在⊙O中$\widehat{AC}$=$\widehat{BD}$,∠AOB=40°,则∠COD的度数( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |
 已知:线段a,直线1及l外一点A.
已知:线段a,直线1及l外一点A.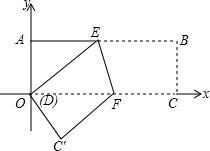 如图,在直角坐标系中,长方形纸片ABCD的边AB∥CO,点B坐标为(9,3),若把图形按如图所示折叠,使B、D两点重合,折痕为EF.
如图,在直角坐标系中,长方形纸片ABCD的边AB∥CO,点B坐标为(9,3),若把图形按如图所示折叠,使B、D两点重合,折痕为EF.