题目内容
小球在如图所示的地板上自由滚动,并随机地停留在某块方砖上,每一块方砖除颜色外完全相同,它最终停留在黑色方砖上的概率是 .

 .
【解析】
试题分析:根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.观察这个图可知:黑色区域(4块)的面积占总面积(9块)的,则它最终停留在黑色方砖上的概率是.
故答案为:.
.
【解析】
试题分析:根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.观察这个图可知:黑色区域(4块)的面积占总面积(9块)的,则它最终停留在黑色方砖上的概率是.
故答案为:.
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
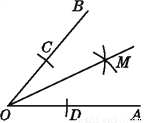
 OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为:OM平分∠BOA.
OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
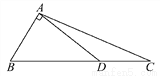
故答案为:OM平分∠BOA. 如图,在直角△BAD中,延长斜边BD到点C,使DC=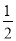 BD,连接AC,若tanB=
BD,连接AC,若tanB=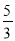 ,则tan∠CAD的值( )
,则tan∠CAD的值( )
A. 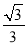 B.
B. 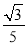 C.
C. 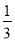 D.
D. 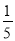
 D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D. 设一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的_____________相同,那么我们就称这个试验的结果是_____________.
 可能性; 等可能的
【解析】【解析】
如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.故答案为:可能性,等可能的.
可能性; 等可能的
【解析】【解析】
如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.故答案为:可能性,等可能的. 如图,转盘中6个小扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向红色区域的概率为 .
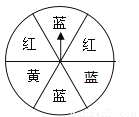
 .
【解析】
试题分析:∵圆被等分成6份,其中红色部分占2份,∴落在阴影区域的概率==,故答案为:.
.
【解析】
试题分析:∵圆被等分成6份,其中红色部分占2份,∴落在阴影区域的概率==,故答案为:. 小杰想用6个除颜色外均相同的球设计一个游戏,下面是他设计的4个游戏方案.不成功的是( )
A. 摸到黄球的概率为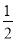 ,红球的概率为
,红球的概率为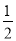
B. 摸到黄、红、白球的概率都为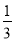
C. 摸到黄球的概率为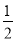 ,红球的概率为
,红球的概率为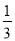 ,白球的概率为
,白球的概率为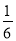
D. 摸到黄球的概率为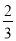 ,摸到红球、白球的概率都是
,摸到红球、白球的概率都是
 D
【解析】解:A.当6个球中有3个黄球,3个红球时,摸到黄球的概率为,红球为,故选项错误;
B.当6个球中有2个黄球,2个红球,2个白球时,摸到黄、红、白球的概率都为,故选项错误;
C.当6个球中有3个黄球,2个红球,1个白球时,摸到黄球的概率为,红球的概率为,白球为,故选项错误;
D. ++>1,故摸到黄球的概率为,摸到红球、白球的概率都是是不成功的,故选项正确.
...
D
【解析】解:A.当6个球中有3个黄球,3个红球时,摸到黄球的概率为,红球为,故选项错误;
B.当6个球中有2个黄球,2个红球,2个白球时,摸到黄、红、白球的概率都为,故选项错误;
C.当6个球中有3个黄球,2个红球,1个白球时,摸到黄球的概率为,红球的概率为,白球为,故选项错误;
D. ++>1,故摸到黄球的概率为,摸到红球、白球的概率都是是不成功的,故选项正确.
... 如图所示,已知B、E分别是线段AC、DF的中点,AC=DF,BF交CD于点H,AE交CD于点G,CH=HG=DG,BH=GE.
(1)填空:因为B、E分别是线段AC、DF的中点,所以CB=________AC,DE=________DF.因为AC=DF,所以CB=________.在△CBH和△DEG中,因为CB=________,CH=________,BH=________EG,所以________≌________(SSS).
(2)除了(1)中的全等三角形外,请你再写出另外一对全等三角形,并说明理由.

 (1) , ,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
【解析】试题分析:(1)因为B是AC的中点, 同理因为AC=DF,由上知根据上面求得: 即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
(2)根据题中条件分析,再用SAS来证明即可
试题解析:(1)因为B是AC的中点, 同理
因为AC=DF,由上知根据上...
(1) , ,DE,DE,DG,△CBH,△DEG. (2)证明见解析.
【解析】试题分析:(1)因为B是AC的中点, 同理因为AC=DF,由上知根据上面求得: 即可得△CBH≌△DEG.两个三角形对应的三边相等,则两个三角形全等,所以找出三角形对应的三边
(2)根据题中条件分析,再用SAS来证明即可
试题解析:(1)因为B是AC的中点, 同理
因为AC=DF,由上知根据上... 如图,在△ABC中,CD是AB边上的高,BE是AC边的高,点O是两条高的交点,则∠A与∠1+∠2的大小关系是( )
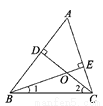
A. ∠A>∠1+∠2 B. ∠A=∠1+∠2
C. ∠A<∠1+∠2 D. 无法确定
 B
【解析】试题解析:∵CD是AB边上的高,BE是AC边上的高,
∴∠OEC=∠ADC=
又∴△ACD和△OCE中,∠ACD=∠OCE,
∴∠A=∠EOC
又∵∠EOC=∠1+∠2,
∴∠A=∠1+∠2.
故选B.
B
【解析】试题解析:∵CD是AB边上的高,BE是AC边上的高,
∴∠OEC=∠ADC=
又∴△ACD和△OCE中,∠ACD=∠OCE,
∴∠A=∠EOC
又∵∠EOC=∠1+∠2,
∴∠A=∠1+∠2.
故选B. 利用基本作图方法,不能作出唯一三角形的是( )
A. 已知两边及其夹角 B. 已知两角及其夹边
C. 已知两边及一边的对角 D. 已知三边
 C
【解析】A. 已知两边及其夹角,作图依据 “SAS”; B. 已知两角及其夹边,作图依据 “ASA”;C. 已知两边及一边的对角,不能做出唯一的三角形; D. 已知三边,作图依据 “SSS”.故选C.
C
【解析】A. 已知两边及其夹角,作图依据 “SAS”; B. 已知两角及其夹边,作图依据 “ASA”;C. 已知两边及一边的对角,不能做出唯一的三角形; D. 已知三边,作图依据 “SSS”.故选C. 
