题目内容
12.在研究反比例函数y=$\frac{a}{x}({a≠0})$的图象时,我们发现有如下性质:(1)图象是中心对称图形,对称中心是原点.
(2)图象是轴对称图形,对称轴是直线y=x,y=-x.
(3)当a>0时,分别在x<0与x>0两个范围内y随x的增大而减小;当a<0时,分别在x<0与x>0两个范围内y随x的增大而增大.类似地我们研究形如:y=$\frac{a}{x-k}$+h(a≠0,k>0,h>0)的函数:
(1)函数y=$\frac{a}{x-k}$+h(a≠0,k>0,h>0)是由反比例函数y=$\frac{a}{x}$(a≠0)向右平移k个单位,再向上平移h个单位得到的.
(2)图象是中心对称图形,对称中心是(k,h).
(3)图象是轴对称图形,对称轴是直线y=x+(h-k)和y=-x+(h+k).
(4)对于函数y=$\frac{3x+6}{2x-4}$,x在哪些范围内,y随x的增大而减小?
答:x<2或x>2.
分析 (1)根据图象平移的法则即可解答;
(2)根据平移的方法,函数y=$\frac{a}{x}$的中心(0,0)平移后的点就是对称中心;
(3)图象平移后与原来的直线y=x和y=-x平行,并且经过对称中心,利用待定系数法即可求解;
(4)把已知的函数y=$\frac{3x+6}{2x-4}$变形成y=$\frac{a}{x-k}$+h(a≠0,k>0,h>0)的形式,类比反比例函数性质即可解答.
解答 解:(1)函数y=$\frac{a}{x-k}$+h(a≠0,k>0,h>0)是由反比例函数y=$\frac{a}{x}$(a≠0)向右平移k个单位,再向上平移h个单位得到的;
(2)图象是中心对称图形,对称中心是(k,h);
(3)设对称轴是y=x+c,把(k,h)代入得h=k+c,
解得:c=h-k,
则对称轴是y=x+(h-k),
设对称轴是y=-x+d,代入(k,h)得h=-k+d,解得d=h+k.
则对称轴是y=-x+(h+k).
故答案是:y=x+(h-k)和y=-x+(h+k);
(4)y=$\frac{3x+6}{2x-4}$=$\frac{3(x-2)+12}{2(x-2)}$=$\frac{6}{x-2}$+$\frac{3}{2}$.
则对称中心是:(2,$\frac{3}{2}$).
则当x<2或x>2时,y随x的增大而减小.
故答案是:x<2或x>2.
点评 本题考查了反比例函数的图象与性质,以及待定系数法求函数的解析式,正确理解图象平移的方法是关键.

练习册系列答案
相关题目
3.数轴上到表示-2的点相距8个单位长度的点所表示的数是( )
| A. | 6 | B. | -10 | C. | ±6 | D. | 6或-10 |
1.下列说法中,错误的是( )
| A. | 四个角都相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线互相垂直的平行四边形是正方形 | |
| D. | 每组邻边都相等的四边形是菱形 |
 秋千长度的长度为3m,秋千向两边摆动时,最大摆角为60度,且两边的摆动角度相同,则它摆置最高处与最低处的高度差为(3-$\frac{3\sqrt{3}}{2}$)米.
秋千长度的长度为3m,秋千向两边摆动时,最大摆角为60度,且两边的摆动角度相同,则它摆置最高处与最低处的高度差为(3-$\frac{3\sqrt{3}}{2}$)米.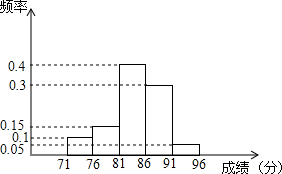 为了了解某校初三年级200名学生的数学毕业考试成绩,从中抽取了20名学生的数学成绩进行分析,下面是根据这20名学生的数学成绩画出的频数分布直方图,如图根据题中给出的条件回答下列问题:
为了了解某校初三年级200名学生的数学毕业考试成绩,从中抽取了20名学生的数学成绩进行分析,下面是根据这20名学生的数学成绩画出的频数分布直方图,如图根据题中给出的条件回答下列问题: