题目内容
已知抛物线y=2x2+n与直线y=2x-1交于点(m,3).
(1)求m和n的值;
(2)求抛物线y=2x2+n的顶点坐标和对称轴;
(3)当x取何值时,二次函数y=2x2+n中y随x的增大而减小;
(4)函数y=2x2+n与直线y=2x-1的图象是否还有其他交点?若有,请求出来;若没有,请说明理由.
(1)求m和n的值;
(2)求抛物线y=2x2+n的顶点坐标和对称轴;
(3)当x取何值时,二次函数y=2x2+n中y随x的增大而减小;
(4)函数y=2x2+n与直线y=2x-1的图象是否还有其他交点?若有,请求出来;若没有,请说明理由.
考点:二次函数的性质
专题:计算题
分析:(1)先把(m,3)代入y=2x-1可求出m,得到交点坐标为(2,3),然后把(2,3)代入y=2x2+n可求出n的值;
(2)、(3)由(1)得抛物线的解析式为y=2x2-5,然后根据二次函数的性质求解;
(4)把直线与抛物线的交点问题转化为方程组的解的问题解决:通过解方程组
判断有没有其他交点.
(2)、(3)由(1)得抛物线的解析式为y=2x2-5,然后根据二次函数的性质求解;
(4)把直线与抛物线的交点问题转化为方程组的解的问题解决:通过解方程组
|
解答:解:(1)把(m,3)代入y=2x-1得2m-1=3,解得m=2,
把(2,3)代入y=2x2+n得2•4+n=3,解得n=-5;
(2)抛物线的解析式为y=2x2-5,它的顶点坐标为(0,-5),对称轴为y轴;
(3)当x<0时,二次函数y=2x2-5中y随x的增大而减小;
(4)有.
解方程组
得
或
,
所以函数y=2x2+n与直线y=2x-1的图象还有一个交点坐标为(-1,-3).
把(2,3)代入y=2x2+n得2•4+n=3,解得n=-5;
(2)抛物线的解析式为y=2x2-5,它的顶点坐标为(0,-5),对称轴为y轴;
(3)当x<0时,二次函数y=2x2-5中y随x的增大而减小;
(4)有.
解方程组
|
|
|
所以函数y=2x2+n与直线y=2x-1的图象还有一个交点坐标为(-1,-3).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
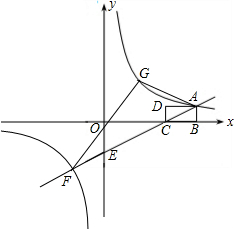 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E.反比例函数y= 已知E为平行四边形ABCD外一点,AE⊥CE,BE⊥DE,求证:平行四边形ABCD是矩形.
已知E为平行四边形ABCD外一点,AE⊥CE,BE⊥DE,求证:平行四边形ABCD是矩形.
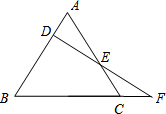 如图,F是等腰三角形ABC的底边BC的延长上一点,且FD⊥AB,垂足为D,交AC于点E,若已知∠F=35°,则∠A=
如图,F是等腰三角形ABC的底边BC的延长上一点,且FD⊥AB,垂足为D,交AC于点E,若已知∠F=35°,则∠A=