题目内容
15．
如图，AB是⊙O的直径，点C、D在⊙O上，若∠CAB=40°，则∠ADC的度数为（ ）| A． | 25° | B． | 30° | C． | 45° | D． | 50° |
分析 由AB是⊙O的直径，根据直径所对的圆周角是直角，可得∠ACD=90°，继而求得∠ABC的度数，然后由圆周角定理，求得∠ADC的?度数．
解答 解：∵AB是⊙O的直径，
∴∠ACB=90°，
∵∠CAB=40°，
∠∠ABC=90°-∠CAB=50°，
∴∠ADC=∠ABC=50°
故选D．
点评 此题考查了圆周角定理．注意直径对的圆周角是直角定理的应用是解此题的关键．
练习册系列答案
相关题目
6．
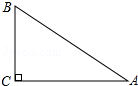如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，那么sinA的值等于（ ）
如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，那么sinA的值等于（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
如图，在一张长为5，宽为4的矩形纸片上，现要剪下一个腰长为3的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为$\frac{9}{2}$或2$\sqrt{2}$或$\frac{3}{2}$$\sqrt{5}$．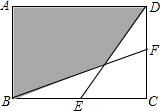
如图，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是32 cm2．
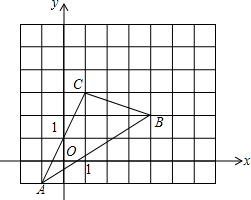如图，△ABC在直角坐标系中，