题目内容
20.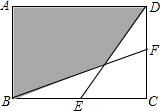 如图,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是32 cm2.
如图,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是32 cm2.
分析 连接BD,EF,可看出阴影部分的面积等于$\frac{1}{2}$正方形的面积+一个三角形DGB的面积,用相似求出三角形的面积,阴影部分的面积可证.
解答 解:连接BD,EF.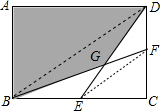
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD=6cm,AD=BC=8cm,
∴△ABD的面积=$\frac{1}{2}$正方形ABCD的面积=$\frac{1}{2}$×6×8=24(cm2),
阴影部分的面积=△ABD的面积+△BDG的面积 (G为BF与DE的交点),
∵△BCD中EF为中位线,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴△GEF∽△GDB,
∴DG=2GE,
∴△BDE的面积=$\frac{1}{2}$△BCD的面积.
∴△BDG的面积=$\frac{2}{3}$△BDE的面积=$\frac{1}{3}$△BCD的面积=$\frac{1}{3}$×24cm2=8cm2,
∴阴影部分的面积=24cm2+8cm2=32cm2,
故答案为32.
点评 本题考查正方形的性质,三角形的面积,中位线性质的应用,注意正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.

练习册系列答案
相关题目
8.某公司的物流业务原来由A运输队承接,已知其收费标准y(元)与运输所跑路程x(公里)之间是某种函数关系.其中部分数据如表所示:
(1)写出y(元)关于x(公里)的函数解析式yA=2.5x;(不需写出定义域)
(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式yB=200+0.9x;(不需写出定义域)
(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式yB=200+0.9x;(不需写出定义域)
(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?
15. 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 50° |
5. 如图所示的立体图形,它的主视图是( )
如图所示的立体图形,它的主视图是( )
 如图所示的立体图形,它的主视图是( )
如图所示的立体图形,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
12.下列四个数中,值最小的数是( )
| A. | tan45° | B. | $\sqrt{3}$ | C. | π | D. | $\frac{8}{3}$ |
 已知圆O,
已知圆O,