题目内容
6.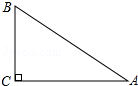 如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,那么sinA的值等于( )
如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,那么sinA的值等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据勾股定理,可得AB的长,根据正弦函数等于对边比斜边,可得答案.
解答 解:由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10.
由正弦函数的定义,得
sinA=$\frac{BC}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$,
故选:C.
点评 本题考查了锐角三角函数的定义,先求出斜边,再求正弦函数.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 方差反映了一组数据的分散或波动的程度 | |
| B. | 数据1,5,3,7,10的中位数是3 | |
| C. | 任何一组数据的平均数和众数都不相等 | |
| D. | 调查一批灯泡的使用寿命适合用全面调查方式 |
18.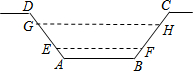 如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
 如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )| A. | 0.55 | B. | 0.8 | C. | 0.6 | D. | 0.75 |
15. 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 50° |
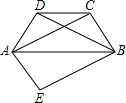 如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.
如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.