题目内容
4.解分式方程:$\frac{{x}^{2}+1}{x}$-$\frac{2x}{{x}^{2}+1}$+1=0.分析 令y=$\frac{{x}^{2}+1}{x}$,则原方程转化为:y$-\frac{2}{y}$+1=0,解得:y1=-2,y2=1,分两种情况,进行求解,即可解答.
解答 解:令y=$\frac{{x}^{2}+1}{x}$,
∴原方程转化为:y$-\frac{2}{y}$+1=0,
方程两边同乘y得:y2+y-2=0,
解得:y1=-2,y2=1,
经检验:y1=-2,y2=1,是方程y$-\frac{2}{y}$+1=0的解,
当y=-2时,即$\frac{{x}^{2}+1}{x}$=-2,
解得:x=-1,
经检验,x=-1是方程的解;
当y=1时,即$\frac{{x}^{2}+1}{x}$=1,此时方程无解;
∴分式方程:$\frac{{x}^{2}+1}{x}$-$\frac{2x}{{x}^{2}+1}$+1=0的解为:x=1.
点评 本题考查了还元法解分式方程,解决本题的关键是令y=$\frac{{x}^{2}+1}{x}$,原方程转化为:y$-\frac{2}{y}$+1=0,即可解答.

练习册系列答案
相关题目
15. 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
 如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,若∠CAB=40°,则∠ADC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 50° |
12.下列四个数中,值最小的数是( )
| A. | tan45° | B. | $\sqrt{3}$ | C. | π | D. | $\frac{8}{3}$ |
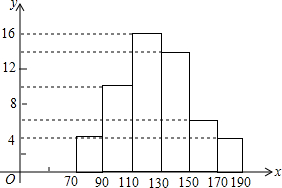 某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是400.
某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是400.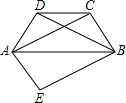 如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.
如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.