题目内容
 如图,在平行四边形ABCD中,对角线AC、BD相交于点0,下列结论:①OA=OC;②∠BAD=∠BCD;③AC=BD;④∠BAD+∠ABC=180°;⑤S△AOB=S△COD,其中正确的结论有
如图,在平行四边形ABCD中,对角线AC、BD相交于点0,下列结论:①OA=OC;②∠BAD=∠BCD;③AC=BD;④∠BAD+∠ABC=180°;⑤S△AOB=S△COD,其中正确的结论有考点:平行四边形的性质
专题:几何图形问题
分析:要熟悉平行四边形的边、角、对角线的性质,根据性质进行判定.
解答:解:根据平行四边形的性质可知:
①平行四边形的对角线互相平分,即OA=OC,正确;
②平行四边形的对角相等,即∠BAD=∠BCD,正确;
③平行四边形的对角线互相平分,不一定相等,错误;
④平行四边形的邻角互补,即∠BAD+∠ABC=180°,正确.
⑤∵在平行四边形ABCD中,对角线AC、BD相交于点0,
∴AO=CO,BO=DO,AB=CD,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,正确,
故答案为:①②④⑤.
①平行四边形的对角线互相平分,即OA=OC,正确;
②平行四边形的对角相等,即∠BAD=∠BCD,正确;

③平行四边形的对角线互相平分,不一定相等,错误;
④平行四边形的邻角互补,即∠BAD+∠ABC=180°,正确.
⑤∵在平行四边形ABCD中,对角线AC、BD相交于点0,
∴AO=CO,BO=DO,AB=CD,
在△AOB和△COD中,
|
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,正确,
故答案为:①②④⑤.
点评:本题考查了平行四边形的面积和性质,解题的关键是掌握平行四边形的性质:对角线互相平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某工厂今年纯利润达到1200亿元,1200亿元用科学记数法表示为( )
| A、1.2×108元 |
| B、1.2×1010元 |
| C、1.2×1011元 |
| D、1.2×109元 |
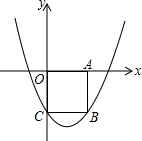 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数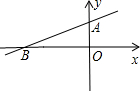 已知如图,直线
已知如图,直线