题目内容
7.观察下列等式:1×$\frac{1}{2}$=1-$\frac{1}{2}$,2×$\frac{2}{3}$=2-$\frac{2}{3}$,3×$\frac{3}{4}$=3-$\frac{3}{4}$,…(1)猜想并写出第n个等式;
(2)证明你写出的等式的正确性.
分析 (1)根据已知等式可得第n个等式为n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$;
(2)根据分式的运算分别计算左右两边,即可验证.
解答 解:(1)由题意知第n个等式为n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$;
(2)左边=n×$\frac{n}{n+1}$=$\frac{{n}^{2}}{n+1}$,
右边=$\frac{{n}^{2}+n}{n+1}$-$\frac{n}{n+1}$=$\frac{{n}^{2}}{n+1}$,
∴左边=右边,即n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$成立.
点评 本题主要考查分式的混合运算,熟练掌握分式的混合运算法则是解题的关键.

练习册系列答案
相关题目
2.要使a5<a3<a<a2<a4成立,则a的取值范围是( )
| A. | 0<a<1 | B. | a>1 | C. | -1<a<0 | D. | a<-1 |
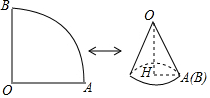 如图,已知扇形AOB的圆心角为90°,面积为16π.
如图,已知扇形AOB的圆心角为90°,面积为16π. 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.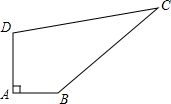 如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四边形ABCD的面积.
如图所示,四边形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四边形ABCD的面积. 如图,△ABC中,AB=AC,D为AB中点,E在AC上,且BE⊥AC,若DE=5,AE=8,则BC的长度为2$\sqrt{10}$.
如图,△ABC中,AB=AC,D为AB中点,E在AC上,且BE⊥AC,若DE=5,AE=8,则BC的长度为2$\sqrt{10}$.