题目内容
9．若关于x的方程x2-2x+m=0有且只有1个实数根，则m=1．分析 根据判别式的意义得到（-2）2-4m=0，然后解关于m的方程即可．
解答 解：根据题意得△=（-2）2-4m=0，
解得m=1．
故答案为1．
点评 本题考查了根的判别式：利用一元二次方程根的判别式（△=b2-4ac）判断方程的根的情况．
练习册系列答案
相关题目
19．
如图，平面内有公共端点的四条射线OA，OB，OC，OD，从射线OA开始按逆时针方向依次在射线上写出数字2，-4，6，-8，10，-12，…则“-2016”在（ ）上．
如图，平面内有公共端点的四条射线OA，OB，OC，OD，从射线OA开始按逆时针方向依次在射线上写出数字2，-4，6，-8，10，-12，…则“-2016”在（ ）上．| A． | 射线OA | B． | 射线OB | C． | 射线OC | D． | 射线OD |
17．
如图，将三个同样的正方形的一个顶点重合放置，如果∠1=45°，∠3=30°时，那么∠2的度数是（ ）
如图，将三个同样的正方形的一个顶点重合放置，如果∠1=45°，∠3=30°时，那么∠2的度数是（ ）| A． | 15° | B． | 25° | C． | 30° | D． | 45° |
4．甲、乙两人分别从相距目的地6km和10km的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20min到达目的地，设甲的速度为3x km/h．依题意，下面所列方程正确的是（ ）
| A． | $\frac{6}{3x}-20=\frac{10}{4x}$ | B． | $\frac{6}{3x}+20=\frac{10}{4x}$ | C． | $\frac{6}{3x}-\frac{1}{3}=\frac{10}{4x}$ | D． | $\frac{6}{3x}+\frac{1}{3}=\frac{10}{4x}$ |
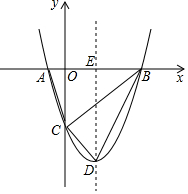如图，抛物线与x轴交于A，B两点，点B坐标是（3，0），与y轴交于点C，顶点D的坐标是（1，-4），对称轴与x轴交于点E
已知，如图，△ABC为等边三角形，CD∥AB．点E、F分别在BC延长线及CD上，∠EAF=60°，联结EF．求证：EF=AF．
如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴、y轴的正半轴上，OA=4，OC=2，点P从点O出发，沿x轴以每秒1个单位的速度向点A匀速运动，到达点A时停止运动，设点P运动的时间是t秒（t＞0），过点P作∠DPA=∠CPO，且PD=$\frac{1}{2}$CP，连接DA．