题目内容
17．
如图，△ABC中，AB=AC，D为AB中点，E在AC上，且BE⊥AC，若DE=5，AE=8，则BC的长度为2$\sqrt{10}$．
分析 由BE⊥AC，D为AB中点，DE=5，根据直角三角形斜边的中线等于斜边的一半，即可求得AB的长，然后由勾股定理求得BC的长．
解答 解：∵BE⊥AC，
∴∠AEB=90°，
∵D为AB中点，
∴AB=2DE=2×5=10，
∵AE=8，
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=6．
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$，
故答案为：2$\sqrt{10}$．
点评 此题考查了直角三角形斜边上的中线的性质以及勾股定理．注意掌握直角三角形斜边的中线等于斜边的一半定理的应用是解此题的关键．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
如图，点M在等边三角形ABC的BC边上，延长BA至N，使AN=MC，连接MN交AC于点O，求证：OM=ON．
如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴、y轴的正半轴上，OA=4，OC=2，点P从点O出发，沿x轴以每秒1个单位的速度向点A匀速运动，到达点A时停止运动，设点P运动的时间是t秒（t＞0），过点P作∠DPA=∠CPO，且PD=$\frac{1}{2}$CP，连接DA．
如图，△ABC中，AD是△ABC的边BC上的高，E、F分别是AB、AC的中点，AC=13、AB=20、BC=21．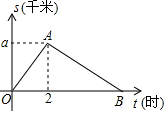
平顶山市教育局举行'重走长征路”健步活动，某教师从起点体育村沿建设路到市生态园．再沿原路返回．该教师离开起点的路程S（千米）与步行时间t（小时）之间的函数关系如图所示．其中从起点到市生态园的平均速度是4千米/小时．用2小时．根据图象提供信息．解答下列问题