题目内容
19.已知m,n满足m+n=4,mn=k-1,设y=(m-n)2(1)当k被5整除时,求证:y能被20整除;
(2)若m,n都为非负数,y存在最大值和最小值吗?若存在,请求之;若不存在,请说明理由.
分析 (1)首先根据k被5整除,可以设k=5t(t是整数),然后根据m+n=4,mn=k-1=5t-1,应用完全平方公式,用含有t的代数式表示出y,判断出y能被20整除即可.
(2)根据m,n都为非负数,以及mn≤${(\frac{m+n}{2})}^{2}$,m+n=4,判断出k的取值范围,即可判断出y是否存在最大值和最小值,如果存在的话,根据二次函数的最值的求法,求出y的最大值和最小值各是多少即可.
解答 (1)证明:当k被5整除时,设k=5t(t是整数),
∵m+n=4,mn=k-1=5t-1,
∴y=(m-n)2
=(m+n)2-4mn
=42-4(5t-1)
=20-20t
=20(1-t)
∵20(1-t)÷20=1-t,
∴y能被20整除.
(2)解:∵m,n都为非负数,
∴mn≥0,
∴k-1≥0,
解得k≥1;
∵mn≤${(\frac{m+n}{2})}^{2}$=${(\frac{4}{2})}^{2}$=4,
∴k-1≤4,
解得k≤5,
∴1≤k≤5,
∴y=(m-n)2
=(m+n)2-4mn
=42-4(k-1)
=20-4k
∵1≤k≤5,
∴4≤4k≤20,
∴0≤20-k≤16,
∴y存在最大值和最小值,最大值是16,最小值是0.
点评 此题主要考查了二次函数的最值的求法,以及完全平方公式的应用,要熟练掌握.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
4.甲、乙两人分别从相距目的地6km和10km的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20min到达目的地,设甲的速度为3x km/h.依题意,下面所列方程正确的是( )
| A. | $\frac{6}{3x}-20=\frac{10}{4x}$ | B. | $\frac{6}{3x}+20=\frac{10}{4x}$ | C. | $\frac{6}{3x}-\frac{1}{3}=\frac{10}{4x}$ | D. | $\frac{6}{3x}+\frac{1}{3}=\frac{10}{4x}$ |
 如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°.
如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°.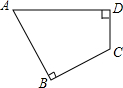 如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长. 已知,如图,△ABC为等边三角形,CD∥AB.点E、F分别在BC延长线及CD上,∠EAF=60°,联结EF.求证:EF=AF.
已知,如图,△ABC为等边三角形,CD∥AB.点E、F分别在BC延长线及CD上,∠EAF=60°,联结EF.求证:EF=AF.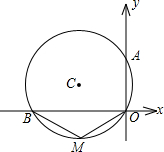 如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.
如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2. 如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.
如图,点M在等边三角形ABC的BC边上,延长BA至N,使AN=MC,连接MN交AC于点O,求证:OM=ON.