题目内容
19. 如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
分析 先根据相似三角形的性质得出$\frac{AC}{CD}$=$\frac{CD}{BC}$,再把AC=3,BC=4代入求出CD的长,进而可得出结论.
解答 解:∵Rt△ADC∽Rt△DBC,AC=3,BC=4,
∴$\frac{AC}{CD}$=$\frac{CD}{BC}$,即$\frac{3}{CD}$=$\frac{CD}{4}$,解得CD=2$\sqrt{3}$,
∴$\frac{AC}{CD}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,即△ADC与△DBC的相似比为$\sqrt{3}$:2.
点评 本题考查的是相似三角形的性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若$\frac{a}{b}=\frac{3}{8}$,则$\frac{a}{a+b}$的值是( )
| A. | $\frac{8}{11}$ | B. | $\frac{6}{13}$ | C. | $\frac{3}{11}$ | D. | $\frac{3}{5}$ |
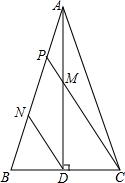 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.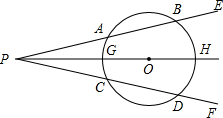 如图,⊙O是∠EPF的平分线上一点,以点O圆心的圆与角的两边分别交于点A,B和点C,D,角平分线PO和⊙O交于点G,H,有下列结论:①AB=CD;②$\widehat{AB}$=$\widehat{CD}$;③PB=PD;④PA=PC.其中正确的有( )
如图,⊙O是∠EPF的平分线上一点,以点O圆心的圆与角的两边分别交于点A,B和点C,D,角平分线PO和⊙O交于点G,H,有下列结论:①AB=CD;②$\widehat{AB}$=$\widehat{CD}$;③PB=PD;④PA=PC.其中正确的有( )