题目内容
9.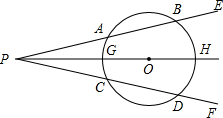 如图,⊙O是∠EPF的平分线上一点,以点O圆心的圆与角的两边分别交于点A,B和点C,D,角平分线PO和⊙O交于点G,H,有下列结论:①AB=CD;②$\widehat{AB}$=$\widehat{CD}$;③PB=PD;④PA=PC.其中正确的有( )
如图,⊙O是∠EPF的平分线上一点,以点O圆心的圆与角的两边分别交于点A,B和点C,D,角平分线PO和⊙O交于点G,H,有下列结论:①AB=CD;②$\widehat{AB}$=$\widehat{CD}$;③PB=PD;④PA=PC.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 过O作OM⊥PB于M,ON⊥PD于N.根据角平分线的性质可知OM=ON,根据垂径定理求得AB=CD,BM=AM=$\frac{1}{2}$AB,ND=CN=$\frac{1}{2}$CD,再利用全等三角形的性质证明PM=PN,进而即可证明PB=PD,PA=PC.
解答 证明:过O作OM⊥PB于M,ON⊥PD于N.
∵OP平分∠EPF,
∴OM=ON,
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
在Rt△POM和Rt△PON中,
$\left\{\begin{array}{l}{OP=OP}\\{OM=ON}\end{array}\right.$,
∴Rt△POM≌Rt△PON(HL),
∴PM=PN,
∵OM⊥AB,ON⊥CD,
∴BM=AM=$\frac{1}{2}$AB,ND=CN=$\frac{1}{2}$CD,
∵AB=CD,
∴BM=DN=AM=CN,
∴PM+BM=PN+DN,PM-AM=PN-CN,
∴PB=PD,PA=PC.
故①AB=CD;②$\widehat{AB}$=$\widehat{CD}$;③PB=PD;④PA=PC都正确,
故选D.
点评 本题考查了角的平分线的性质、垂径定理和三角形全等的判定和性质;角的平分线的性质:角的平分线上的点到角的两边的距离相等;在同圆中两弦的弦心距相等,则弦长相等.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
17.解方程(x+1)(x+3)=5较为合适的方法( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法或配方法 | D. | 分解因式法 |
4.一艘轮船从港口A出发向东北方向航行7km,另一艘轮船也从港口A出发向东南方向航行了12km,此时两艘轮船相距( )
| A. | 5km | B. | $\sqrt{193}$km | C. | 19km | D. | 193km |
14.下列说法错误的是( )
| A. | 若ab>0,则$\frac{b}{a}>0$ | B. | 若$\frac{b}{a}<0$,则ab<0 | ||
| C. | 若ac<0,$\frac{ab}{c}>0$,则b<0 | D. | 若ac>0,bc>0,则abc>0 |
1.抛物线y=$\frac{1}{2}$(x+2)(x-6)的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=6 | C. | 直线x=2 | D. | 直线x=4 |
 如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比. 如图,在平面直角坐标系xOy中,抛物线C1:y=a(x-$\frac{5}{2}$)2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.
如图,在平面直角坐标系xOy中,抛物线C1:y=a(x-$\frac{5}{2}$)2+h分别与x轴、y轴交于点A(1,0)和点B(0,-2),将线段AB绕点A逆时针旋转90°至AP.