题目内容
10.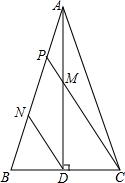 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点M是线段AD的中点,CM交AB于点P,DN∥CM交AB于点N,若AB=6,求PN的长.
分析 根据等腰三角形三线合一的性质得到BD=DC,根据三角形中位线定理得到PN=$\frac{1}{3}$AB,计算得到答案.
解答 解:∵AB=AC,AD⊥BC,
∴BD=DC,又DN∥CM,
∴BN=NP,
∵点M是线段AD的中点,DN∥CM,
∴NP=PA,
∴PN=$\frac{1}{3}$AB=2.
点评 本题考查的是三角形中位线定理和等腰三角形的性质,掌握经过三角形一边的中点平行于另一边的直线,平分第三边是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.下列运算结果为正数的是( )
| A. | 1-24×5 | B. | -24×5 | C. | (-2)4×5 | D. | 1-24 |

 如图,图中数轴的单位长度为1.
如图,图中数轴的单位长度为1.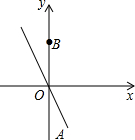 已知正比例函数过点A(2,-4),点P在正比例函数图象上,B(0,4)且S△ABP=8.
已知正比例函数过点A(2,-4),点P在正比例函数图象上,B(0,4)且S△ABP=8. 如图,DE⊥AB于E,∠A=40°,∠D=30°,求∠ACD的度数.
如图,DE⊥AB于E,∠A=40°,∠D=30°,求∠ACD的度数. 如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.
如图,Rt△ADC∽Rt△DBC,AC=3,BC=4,试求△ADC与△DBC的相似比.