题目内容
6.对于抛物线y=-4x+x2-7,有下列说法:①抛物线的开口向上;②对称轴为x=2;③顶点坐标为(2,-3);④点(-$\frac{1}{2}$,-9)在抛物线上.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 先把抛物线解析式配成顶点式,然后根据二次函数的性质对①②③进行判断;根据二次函数图象上点的坐标特征对④进行判断.
解答 解:∵y=x2-4x-7=(x-2)2-11,
∴抛物线开口向上,所以①正确;
抛物线对称轴为直线x=2,所以②正确;
抛物线顶点坐标为(2,-11),所以③错误;
∵x=-$\frac{1}{2}$时,y=(x-2)2-11=(-$\frac{1}{2}$-2)2-11=-$\frac{19}{4}$,
∴点(-$\frac{1}{2}$,-9)不在抛物线上,所以④错误.
故选B.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-b2a时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
14.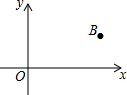 在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
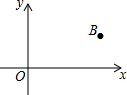 在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )
在直角坐标系中,点B的坐标为(3,1),则点B关于原点成中心对称的点的坐标为( )| A. | (3,-1) | B. | (-3,1) | C. | (-1,-3) | D. | (-3,-1) |
1.若a满足不等式组$\left\{\begin{array}{l}{2a-1≤1}\\{\frac{1-a}{2}>2}\end{array}\right.$,则关于x的方程(a-2)x2-(2a-1)x+a+$\frac{1}{2}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 以上三种情况都有可能 |
18.一组数据:2,3,6,6,7,8,8,8的中位数是( )
| A. | 6 | B. | 6.5 | C. | 7 | D. | 8 |
 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=32°.
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=32°.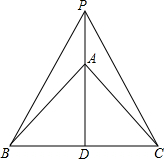 如图,AD是等腰直角三角形ABC斜边上的中线,P是DA延长线上的一点,当∠PBA=15°时,△PBC是等边三角形.
如图,AD是等腰直角三角形ABC斜边上的中线,P是DA延长线上的一点,当∠PBA=15°时,△PBC是等边三角形.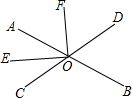 如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.
如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.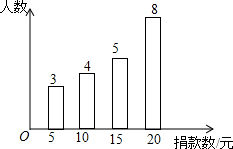 某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,根据这组数据绘制成如图所示的统计图.