题目内容
11．
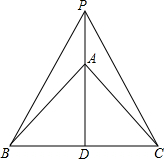如图，AD是等腰直角三角形ABC斜边上的中线，P是DA延长线上的一点，当∠PBA=15°时，△PBC是等边三角形．
分析 根据等腰直角三角形的性质得出∠ABC=45°，利用一个角是60°的等腰三角形是等边三角形解答即可．
解答 解：当∠PBA=15°时，△PBC是等边三角形，
理由如下：
∵AD是等腰三角形ABC斜边上的中线，
∴∠ABC=45°，BD=DC，AD⊥BC，
∴PB=PC，
∵∠PBA=15°，
∴∠PBC=60°，
∴△PBC是等边三角形，
故答案为：15°
点评 此题考查等边三角形的判定，关键是根据一个角是60°的等腰三角形是等边三角形解答．
练习册系列答案
相关题目
1．
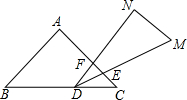一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角形的斜边上，AC与DM，DN分别交于点E，F，把△DEF绕点D旋转到一定位置，使得DE=DF，则∠BDN的度数是（ ）
一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角形的斜边上，AC与DM，DN分别交于点E，F，把△DEF绕点D旋转到一定位置，使得DE=DF，则∠BDN的度数是（ ）| A． | 105° | B． | 115° | C． | 120° | D． | 135° |
19．
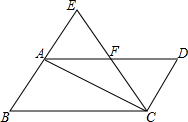如图，在平行四边形ABCD中，∠B=60°，将△ABC沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有（ ）
如图，在平行四边形ABCD中，∠B=60°，将△ABC沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
6．对于抛物线y=-4x+x2-7，有下列说法：①抛物线的开口向上；②对称轴为x=2；③顶点坐标为（2，-3）；④点（-$\frac{1}{2}$，-9）在抛物线上．其中正确的有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
16．$\sqrt{2}$的相反数是（ ）
| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
3．
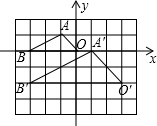如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（ ）
如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（ ）| A． | （0，0） | B． | （0，1） | C． | （-3，2） | D． | （3，-2） |