题目内容
15.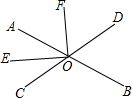 如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.
如图,O是直线AB上一点,过O作射线OE、OF.OE平分∠AOC,∠AOC=∠BOD.(1)试说明∠AOC和∠BOD的对顶角;
(2)若OE⊥OF,试说明OF平分∠AOD.
分析 (1)根据平角的定义得到∠AOD+∠BOD=180°,由等量代换得到∠AOC+∠AOD=180°,于是得到C,O,D三点共线,问题得证;
(2)由OE平分∠AOC,得到∠AOE=∠COE,根据垂直的定义得到∠EOF=90°,于是得到∠AOE+∠AOF=90°,∠COE+∠DOF=90°,推出∠AOF=∠DOF,问题得证.
解答 解:(1)∵∠AOD+∠BOD=180°,
∵∠AOC=∠BOD,
∴∠AOC+∠AOD=180°,
∴C,O,D三点共线,
∴∠AOC和∠BOD是对顶角;
(2)∵OE平分∠AOC,
∴∠AOE=∠COE,
∵OE⊥OF,
∴∠EOF=90°,
∴∠AOE+∠AOF=90°,
∴∠COE+∠DOF=90°,
∴∠AOF=∠DOF,
∴OF平分∠AOD.
点评 本题考查了对顶角、邻补角的定义,角平分线的性质,垂直的定义,正确的识图是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.对于抛物线y=-4x+x2-7,有下列说法:①抛物线的开口向上;②对称轴为x=2;③顶点坐标为(2,-3);④点(-$\frac{1}{2}$,-9)在抛物线上.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.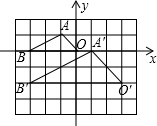 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )| A. | (0,0) | B. | (0,1) | C. | (-3,2) | D. | (3,-2) |
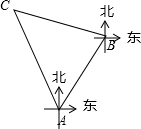 某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).
某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).