题目内容
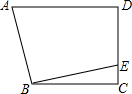 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )| A、6 | B、8 | C、10 | D、无法确定 |
考点:全等三角形的判定与性质,矩形的判定与性质
专题:
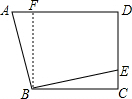
分析:作BF⊥AD与F,就可以得出BF∥CD,就可以得出四边形BCDF是矩形,进而得出四边形BCDF是正方形,就有BF=BC,证明△BCE≌△BAF就可以得出AF=CE,进而得出结论.
解答:解:作BF⊥AD与F,
∴∠AFB=BFD=90°,
∵AD∥BC,
∴∠FBC=∠AFB=90°,
∵∠C=90°,
∴∠C=∠AFB=∠BFD=∠FBC=90°.
∴四边形BCDF是矩形.
∵BC=CD,
∴四边形BCDF是正方形,
∴BC=BF=FD.
∵EB⊥AB,
∴∠ABE=90°,
∴∠ABE=∠FBC,
∴∠ABE-∠FBE=∠FBC-∠FBE,
∴∠CBE=∠FBA.
在△BCE和△BAF中
,
∴△BCE≌△BAF(ASA),
∴CE=FA.
∵CD=BC=8,DE=6,
∴DF=8,CE=2,
∴FA=2,
∴AD=8+2=10.
故选C.
∴∠AFB=BFD=90°,
∵AD∥BC,
∴∠FBC=∠AFB=90°,
∵∠C=90°,
∴∠C=∠AFB=∠BFD=∠FBC=90°.
∴四边形BCDF是矩形.
∵BC=CD,
∴四边形BCDF是正方形,
∴BC=BF=FD.
∵EB⊥AB,
∴∠ABE=90°,
∴∠ABE=∠FBC,
∴∠ABE-∠FBE=∠FBC-∠FBE,
∴∠CBE=∠FBA.
在△BCE和△BAF中
|
∴△BCE≌△BAF(ASA),
∴CE=FA.
∵CD=BC=8,DE=6,
∴DF=8,CE=2,
∴FA=2,
∴AD=8+2=10.
故选C.

点评:本题考查了平行线的性质的运用,矩形的判定及性质的运用,正方形的盘点机性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )| A、4 | B、6 | C、8 | D、10 |
已知不等式-x+5>3x-3的解集是2<x,则直线y=-x+5与y=3x-3的交点坐标是( )
| A、(2,3) |
| B、(3,2) |
| C、(3,-2) |
| D、(-3,2) |
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
| A、第一次右拐50°,第二次左拐130° |
| B、第一次左拐50°,第二次右拐50° |
| C、第一次左拐50°,第二次左拐130° |
| D、第一次右拐50°,第二次右拐50° |
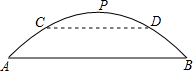 如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米,
如图,有一座拱桥是抛物线形,它的跨度AB为60米,拱桥最高处点P到AB的距离为18米, 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,将线段AB绕点B顺时针旋转90°.将线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,将线段AB绕点B顺时针旋转90°.将线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.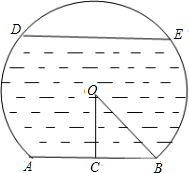 一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=