题目内容
1．设点A（-3，a），B（b，$\frac{1}{2}$）在同一个正比例函数的图象上，则ab的值为（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{3}{2}$ | C． | -6 | D． | $\frac{3}{2}$ |
分析 运用待定系数法求得正比例函数解析式，进一步求得a和b的值，从而求解．
解答 解：设解析式为：y=kx，
将点（-3，a）代入可得：-3k=a，
把点（b，$\frac{1}{2}$）代入可得，bk=$\frac{1}{2}$，
解得ab=-$\frac{3}{2}$
故选B．
点评 此题考查了一次函数图象上点的坐标特征，此类题目需灵活运用待定系数法建立函数解析式，然后将点的坐标代入解析式，利用方程解决问题．
练习册系列答案
相关题目
11．
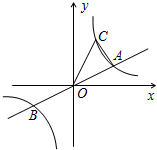如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A、B两点，点B的坐标为（-4，-2），C为双曲线y=$\frac{k}{x}$（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（ ）
如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）交于A、B两点，点B的坐标为（-4，-2），C为双曲线y=$\frac{k}{x}$（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（ ）| A． | （2，4） | B． | （1，8） | C． | （2，4）或（1，8） | D． | （2，4）或（8，1） |
12．
如图，已知小鱼与大鱼是位似图形，则小鱼的点（a，b）对应大鱼的点（ ）
如图，已知小鱼与大鱼是位似图形，则小鱼的点（a，b）对应大鱼的点（ ）| A． | （-a，-2b） | B． | （-2a，-b） | C． | （-2b，-2a） | D． | （-2a，-2b） |
9．两个相似五边形的相似比为 2：3，则它们的面积比为（ ）
| A． | 2：3 | B． | 3：2 | C． | 4：9 | D． | 9：4 |
16．sin60°的值等于（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{3}}{2}$ |
6．下列事件中，必然事件是（ ）
| A． | 打开电视，正在播放新闻 | B． | 抛一枚硬币，正面朝上 | ||
| C． | 明天会下雨 | D． | 地球绕着太阳转 |
