题目内容
12.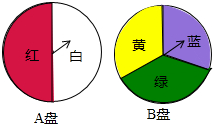 小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.
分析 (1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(2)首先由(1)中的表格求得配成紫色和两个转盘转出同种颜色的概率,即可得知这个约定对双方是否公平.
解答 解:(1)列表得:
| 第二个转盘 第一个转盘 | 黄 | 蓝 | 绿 |
| 红 | (红,黄) | (红,蓝) | (红,绿) |
| 白 | (白,黄) | (白,蓝) | (白,绿) |
(2)这个游戏不公平,理由如下:
由(1)可知配成紫色的概率=$\frac{1}{6}$;两个转盘转出同种颜色概率=0,
所以游戏不公平.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.1微米=0.000001米,1微米用科学记数法可表示为( )米.
| A. | 1×106 | B. | 1×105 | C. | 1×10-5 | D. | 1×10-6 |
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
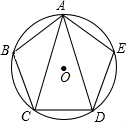 如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)
如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)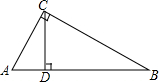 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值. 如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.
如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8. 如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.
如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.