题目内容
1．
如图，点M，N在线段AC上，AM=CN，AB∥CD，AB=CD，试说明∠1=∠2．
分析 首先证明△ABM≌△CDN得到BM=DN，∠AMB=∠DNC，再证明△BMN≌△DNM即可．
解答 证明：∵AB∥CD，
∴∠A=∠C，
在△ABM和△CDN中，
$\left\{\begin{array}{l}{AB=CD}\\{∠A=∠C}\\{AM=CN}\end{array}\right.$，
∴△ABM≌△CDN，
∴BM=DN，∠AMB=∠DNC，
∵∠AMB+∠BMN=180°，∠DNC+∠MND=180°，
∴∠BMN=∠DNM，
在△BMN和△DNM中，
$\left\{\begin{array}{l}{MN=MN}\\{∠BMN=∠DNM}\\{MB=DN}\end{array}\right.$，
∴△BMN≌△DNM，
∴∠1=∠2．
点评 本题考查全等三角形的判定和性质，解题的关键是两次利用三角形全等，属于中考常考题型．
练习册系列答案
相关题目
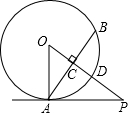如图，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA=2，OP=4，则弦AB的长2$\sqrt{3}$．
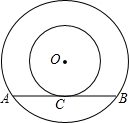如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，求弦AB的长．
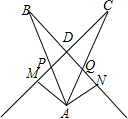已知AB=AC，P，Q分别是AB，AC上各点，且BP=CQ，AM⊥CP交CP延长线于M，AN⊥BQ交BQ延长线于N，说明AM=AN．
已知，如图，线段AC，BD交于O，∠AOB为钝角，AB=CD，BF⊥AC于F，DE⊥AC于E，AE=CF，
