题目内容
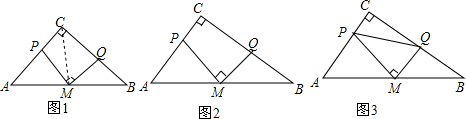
10.在Rt△ABC中,∠C=90°,M是AB的中点,PM⊥MQ,P,Q分别在边AC,BC上.(1)尝试探究:在如图1中,若AC=BC,连结CM后,请探究PM与MQ的数量关系是PM=MQ,并加以证明;
(2)类比延伸:如图2,在原题条件下,BC=kAC,试探究PM与MQ的数量关系是PM=kMQ;
(3)拓展探究:如图3,在原题条件下,试写出AP,PQ,BQ三者之间的关系PA2+BQ2=PQ2.
分析 (1)结论:PM=PQ,图1中,连接MC,根据等腰直角三角形的性质得到∠B=∠ACM,CM=BM=$\frac{1}{2}$AB,∠CMB=90°,根据余角的性质得到∠PMC=∠BMQ,推出△PMC≌△BMQ,根据全等三角形的性质即可得到结论.
(2)结论:PM=kMQ,图2中,作MF⊥BC,ME⊥C垂足分别为F、E,由△PMQ∽△FMQ得$\frac{PM}{MF}=\frac{EM}{MF}$,因为AM=MB,MF∥CA,ME∥BC,所以BF=CF,AE=EC,所以EM=$\frac{1}{2}$BC,MF=$\frac{1}{2}$AC,即可得出结论.
(3)结论:PA2+BQ2=PQ2,图3中,延长PM到E使得PM=ME,连接BE,QE,由△AMP≌△BME得AP=BE,∠A=∠MBE,再证明∠QBE=90°,在RT△BQE中利用勾股定理即可.
解答 (1)结论:PM=MQ,理由如下:
证明:∵△ABC是等腰直角三角形,
∴∠B=45°,
∵M是AB的中点,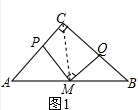
∴∠ACM=45°,
∴∠B=∠ACM,CM=BM=$\frac{1}{2}$AB,∠CMB=90°,
∵∠EMD=90°,
∴∠PMC=∠BMQ,
在△PMC与△BMQ中,$\left\{\begin{array}{l}{∠PMC=∠BMQ}\\{CM=BM}\\{∠PCM=∠B}\end{array}\right.$,
∴△PMC≌△BMQ,
∴MP=MQ.
故答案为PM=MQ.
(2)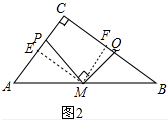 结论:PM=kMQ,利用如下:
结论:PM=kMQ,利用如下:
证明:作MF⊥BC,ME⊥C垂足分别为F、E.
∵∠MEC=∠C=∠MFC=90°,
∴四边形MFCE是矩形,
∴∠EMF=∠PMQ=90°,
∴∠EMP=∠FMQ,
∴△PMQ∽△FMQ,
∴$\frac{PM}{MQ}=\frac{EM}{MF}$,
∵AM=MB,MF∥CA,ME∥BC,
∴BF=CF,AE=EC,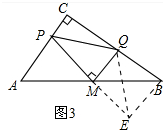
∴EM=$\frac{1}{2}$BC,MF=$\frac{1}{2}$AC,
∴$\frac{PM}{MQ}=\frac{EM}{MF}$=$\frac{BC}{AC}=k$.
∴PM=kMQ.
故答案为PM=kMQ.
(3)结论:PA2+BQ2=PQ2理由如下:
证明:延长PM到E使得PM=ME,连接BE,QE.
在△AMP和△BME中,
$\left\{\begin{array}{l}{AM=MB}\\{∠AMP=∠BME}\\{PM=ME}\end{array}\right.$,
∴△AMP≌△BME,
∴AP=BE,∠A=∠MBE,
∵PM=ME,QM⊥PE,
∴QP=PE,
∵∠A+∠ABC=90°,
∴∠ABC+∠MBE=90°,
∴∠QBE=90°,
∴QE2=QB2+BE2,
∴PA2+BQ2=PQ2.
故答案为PA2+BQ2=PQ2.
点评 本题考查全等三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识,构造全等三角形是解决问题的关键,属于中考常考题型.

| A. | ①②④ | B. | ①②⑤ | C. | ②③⑤ | D. | ①②③⑤ |
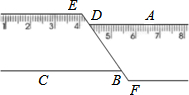 如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )
如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 125° |

 如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.
如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.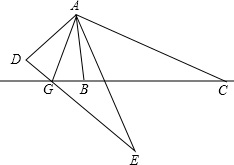 如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.
如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.

 如图,铁路AB两旁有两城分别在C、D处,为利于推动经济发展,他们都要求在距自己城市最近的A、B处建立火车站,经协商铁道部门最后在与C、D距离相等的E处修建了一个火车站.如果CA=10km,DB=30km,AB=50km.
如图,铁路AB两旁有两城分别在C、D处,为利于推动经济发展,他们都要求在距自己城市最近的A、B处建立火车站,经协商铁道部门最后在与C、D距离相等的E处修建了一个火车站.如果CA=10km,DB=30km,AB=50km.