题目内容
13. 已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,
已知,如图,线段AC,BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF,(1)求证:BO=DO.
(2)若∠AOB为锐角,其他条件不变,请画出图象并判断(1)中的结论是否仍成立.
分析 (1)由AE=CF得AF=EC,可以根据HL得到△ABF≌△CDE即可证明.
(2)结论成立,证明方法类似(1)略.
解答 (1)证明∵AE=CF,
∴AF=EC,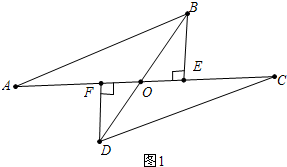
∵BF⊥AC于F,DE⊥AC于E,
∴∠AFB=∠DEC=90°,
在RT△ABF和RT△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$,
∴△ABF≌△CDE,
∴BF=DE,
在△BFO和△DEO中,
$\left\{\begin{array}{l}{∠BOF=∠DOE}\\{∠BFO=∠DEO}\\{BF=DE}\end{array}\right.$,
∴△BFO≌△DEO,
∴BO=OD.
(2)如图2结论不变,理由如下,
证明∵AE=CF,
∴AF=EC
∵BF⊥AC于F,DE⊥AC于E,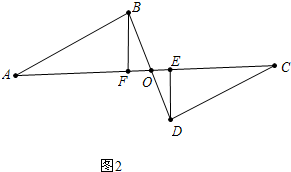
∴∠AFB=∠DEC=90°,
在RT△ABF和RT△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=CE}\end{array}\right.$,
∴△ABF≌△CDE,
∴BF=DE,
在△BFO和△DEO中,
$\left\{\begin{array}{l}{∠BOF=∠DOE}\\{∠BFO=∠DEO}\\{BF=DE}\end{array}\right.$,
∴△BFO≌△DEO,
∴BO=OD.
点评 本题考查全等三角形的判定和性质,解题的关键是两次利用全等三角形,属于中考常考题型.

练习册系列答案
相关题目
19.已知m-n=-2,则代数式10-m+n=( )
| A. | 8 | B. | 12 | C. | -8 | D. | -12 |
20.下列运算中正确的是( )
| A. | (-a)2•a3=a6 | B. | -a8÷a4=-a2 | C. | $\sqrt{4}$=±2 | D. | (-2a2)3=-8a6 |
2.下列各式①26÷22=24;②(23)2=26;③105×10-5=0;④(x-1)2=x2-1;⑤(-a)3=-a3,其中计算正确的是( )
| A. | ①②④ | B. | ①②⑤ | C. | ②③⑤ | D. | ①②③⑤ |
 如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.
如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.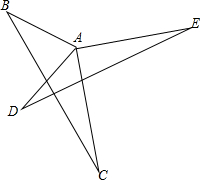 如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明:
如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明: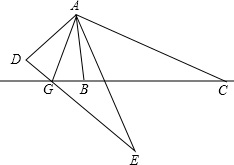 如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.
如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.