如图.以O为圆心的两个同心圆中.大圆的弦AB与小圆相切于点C.若大圆半径为10cm.小圆半径为6cm.求弦AB的长．题目和参考答案——青夏教育精英家教网—

题目内容

8．

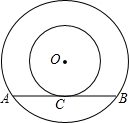如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，求弦AB的长．

分析连接OA、OC根据切线的性质可知△OAC是直角三角形，OC垂直平分AB，根据勾股定理及垂径定理即可解答．

解答解：连接OA、OC，
∵AB是小圆的切线，
∴OC⊥AB，
∵OA=10cm，OC=6cm，
∴AC=$\sqrt{A{O}^{2}-O{C}^{2}}$=8cm，
∵AB是大圆的弦，OC过圆心，OC⊥AB，
∴AB=2AC=2×8=16cm．

点评本题考查了切线的性质，解答此题的关键是连接OA、OC，构造出直角三角形，利用切线的性质及勾股定理解答．

练习册系列答案

同步练习强化拓展系列答案

一课一练天津人民美术出版社系列答案

花山小状元课时练初中生100全优卷系列答案

一课一练文心出版社系列答案

海豚图书中考必备系列答案

授之以渔全国各省市中考试题精选系列答案

相关题目

18．

如图，点B的坐标（4，4），过点B作BA⊥x轴，垂足为A，作BC⊥y轴，垂足为C，反比例函数y=$\frac{k}{x}$（k＞0）的图象经过BC的中点E，与AB交于点F，分别连接OE、CF，其交点为M，连接AM．求证：AM=AO．

19．已知m-n=-2，则代数式10-m+n=（　　）

16．阅读：已知如图（1）△ABC中，AB=AC，CF为AB边上的高，P为BC边上的一个动点，PD⊥AB，PE⊥AC，探究PD、PE和CF之间的关系．聪明的小强连接AP通过S_△APB+S_△APC=S_△ABC，从而发现PD+PE=CF．
理解：小强对上述问题进一步进行探究，当点P在BC延长线上时，如图2，其它条件不变，发现PD-PE=CF，请你证明小强的这一发现．
运用（一）：如图3，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，P为折痕EF上的任意一点，PG⊥BE，PH⊥BC，若AD=8，CF=3，求PG+PH的值．
运用（二）：如图4，四边形ABCD中，E为AD边上的点，且EB⊥AB，CE⊥CD，且AB•CE=CD•BE，M、N分别为AE、DE的中点，若AD=10，sinA=$\frac{3}{5}$，求△BEM与△CEN的周长之和．

3．下列长度的3根小棒，能搭成三角形的是（　　）

13．

如图，四边形ABCD中，AB∥CD，BC⊥CD，E是AD的中点，连结BE并延长交CD的延长线于点F．
（1）请连结AF、BD，试判断四边形ABDF是何种特殊四边形，并说明理由．
（2）若AB=4，BC=5，CD=6，求△BCF的面积．

-a⁸÷a⁴=-a²

1．

如图，点M，N在线段AC上，AM=CN，AB∥CD，AB=CD，试说明∠1=∠2．

2．下列各式①2⁶÷2²=2⁴；②（2³）²=2⁶；③10⁵×10^-5=0；④（x-1）²=x²-1；⑤（-a）³=-a³，其中计算正确的是（　　）

试题分类