题目内容
5.(1)如图1,一住宅楼发生火灾,消防车立即赶到准备在距大厦6米处升起云梯到火灾窗口展开营救,已知云梯AB长15米,云梯底部B距地面2米,此时消防队员能否成功救下等候在距离地面约14米窗口的受困人群?说说你的理由.(2)如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
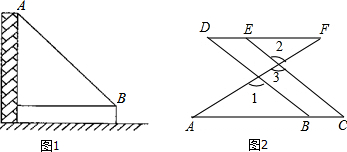
分析 (1)先根据题意建立直角三角形,然后利用勾股定理求出AB的长度,最后于云梯的长度比较即可得出答案.
(2)由已知条件和对顶角相等得出∠1=∠3,证出BD∥CE,由平行线的性质得出∠ABD=∠C,在证出∠ABD=∠D,得出AC∥DF,由平行线的性质即可得出结论.
解答 (1)解: 能救下.理由如下:如图所示:
能救下.理由如下:如图所示:
由题意得,BC=6米,AC=14-2=12米,
在RT△ABC中,AB2=AC2+BC2,
∴AB2=(14-2)2+62=144+36=180,
而152=225>180,
故能救下.
(2)证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠A=∠F.
点评 此题考查了勾股定理的应用、平行线的判定与性质;熟练掌握勾股定理和平行线的判定与性质,在(1)中,根据题意得出AC、BC的长度,利用勾股定理求出AB是解答本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.下列运算中正确的是( )
| A. | (-a)2•a3=a6 | B. | -a8÷a4=-a2 | C. | $\sqrt{4}$=±2 | D. | (-2a2)3=-8a6 |
19.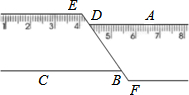 如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )
如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )
 如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )
如图,一把长方形直尺沿直线断开并错位后,王丽同学发现点E、D、B、F在同一条直线上,若∠ADE=115°,则∠DBC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 125° |

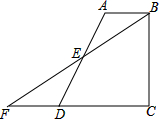 如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.
如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F. 如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.
如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.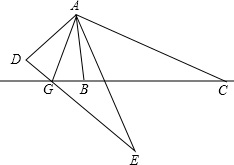 如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.
如图,△ABC外有E,D两点,DE=BC,EA=CA,∠ABC=∠ADE=90°,连接DE交CB的延长线于点G,连接AG,求证:GA平分∠DGB.