题目内容
19.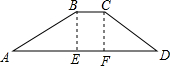 如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积.
如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积.
分析 根据坡比定义求得AE=50、DF=40,从而得出梯形的下底AD的长,由梯形面积公式求解可得.
解答 解:根据题意知BC=EF=5,BE=CF=20,
∵$\frac{BE}{AE}$=$\frac{1}{2.5}$,$\frac{CF}{DF}$=$\frac{1}{2}$,
∴AE=2.5BE=50,DF=2CF=40,
则AD=AE+EF+DF=50+5+40=95,
∴S梯形ABCD=$\frac{1}{2}$×(BC+AD)×BE=$\frac{1}{2}$×(5+95)×20=1000(平方米),
答:大坝的截面面积为1000平方米.
点评 本题主要考查解直角三角形的应用-坡度坡角问题,熟练掌握坡比的定义和梯形的面积公式是解题的关键.

练习册系列答案
相关题目
9.若点A(2,n)在x轴上,则点B(-2,n+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.函数y=$\frac{x-2}{x+1}$+x中x的取值范围为( )
| A. | x≠1 | B. | x≠-1 | C. | x≠-2 | D. | x≠2 |
9. 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )| A. | y=2x+2 | B. | y=2x-2 | C. | y=-3x+3 | D. | y=-x-4 |
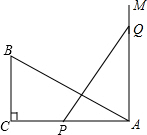 如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm.一条线段PQ=AB,并且P、Q两点分别在线段AC和过A点且垂直于AC的射线AM上运动.问当P点位于AC的什么位置时由P、Q、A点构成的三角形与△ABC全等?并说明理由. 如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米?
如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米? 如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.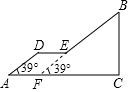 如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.
如图,人行天桥的引桥由楼梯和一段水平平台构成,楼梯AD与地面成39°,DE∥AC,楼梯EB与水平地面成39°角,已知BC=6m,AC=11m.