题目内容
4.已知在Rt△ABC中,∠ABC=90°,点P是AC的中点.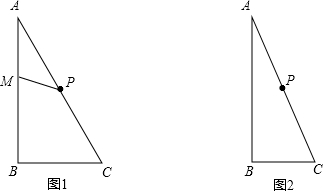
(1)当∠A=30°且点M、N分别在线段AB、BC上时,∠MPN=90°,请在图1中将图形补充完整,并且直接写出PM与PN的比值;
(2)当∠A=23°且点M、N分别在线段AB、BC的延长线上时,(1)中的其他条件不变,请写出PM与PN比值的思路.
分析 (1)补充图形如图1所示,过P作PE⊥AB于E,PF⊥BC于F,得到四边形PEBF是矩形,根据矩形的性质得到PE∥BC,PF∥AB,根据三角形的中位线的性质得到PE=$\frac{1}{2}$BC,PF=$\frac{1}{2}$AB,根据相似三角形的性质即可得到结论;
(2)过点P作PE⊥AB于E,PF⊥BC于点F,由PF⊥BC和∠ABC=90°可以得到AB∥PF,∠PFC=90°进而得到∠A=∠FPC;根据全等三角形的性质得到AE=PF;根据相似三角形的判定和性质即可得到结论.
解答  解:(1)补充图形如图1所示,过P作PE⊥AB于E,PF⊥BC于F,
解:(1)补充图形如图1所示,过P作PE⊥AB于E,PF⊥BC于F,
∵∠ABC=90°,
∴四边形PEBF是矩形,
∴PE∥BC,PF∥AB,
∵P是AC的中点,
∴PE=$\frac{1}{2}$BC,PF=$\frac{1}{2}$AB,
∵∠A=30°,
∴$\frac{PE}{PF}$=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$,
∵∠EPF=∠MPN=90°,
∴∠MPE=∠NPF,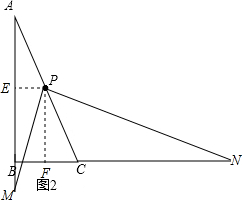
∴△PEM∽△PFN,
∴$\frac{PM}{PN}$=$\frac{PE}{PF}$=$\frac{\sqrt{3}}{3}$;
(2)思路:在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F,
由PF⊥BC和∠ABC=90°可以得到AB∥PF,∠PFC=90°进而得到
∠A=∠FPC;由∠PFC=∠AEP=90°,AP=PC可以得到
△AEP≌△PFC,进而推出AE=PF;
由点P处的两个直角可以得到∠EPM=∠FPN,
进而可以得到△MEP∽△NPF,由此可以得到$\frac{PF}{PE}$=$\frac{PN}{PM}$
等量代换可以得到$\frac{PM}{PN}=\frac{PE}{AE}$;在Rt△AEP中$tan∠A=\frac{PE}{AE}$,可以得到$\frac{PM}{PN}=tan23°$.
解:点P作PE⊥AB于E,PF⊥BC于点F,
则四边形PEBF是矩形,
∴PF∥AB,∠EPF=90°,
∴∠A=∠CPF=23°,
在△AEP与△PFC中,$\left\{\begin{array}{l}{∠A=∠CPF}\\{∠AEP=∠PFC}\\{AP=PC}\end{array}\right.$,
∴△AEP≌△PFC,
∴AE=PF,
∵∠EPF=∠MPN=90°,
∴∠EPM=∠FPN,
∴△MEP∽△NPF,
∴$\frac{PF}{PE}=\frac{PN}{PM}$,
∴$\frac{PM}{PN}=\frac{PE}{AE}$,
∵tan∠A=$\frac{PE}{AE}$,
∴$\frac{PM}{PN}$=tan23°.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
 已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )
已知一次函数y=kx+b的图象如图所示,则该函数的表达式可能是( )| A. | y=2x+2 | B. | y=2x-2 | C. | y=-3x+3 | D. | y=-x-4 |
 如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD.
如图,已知:∠1=∠2,AC=AE,BC=DE,且点D在BC上,求证:AB=AD. 如图,点(3,m)为直线AB上的点.求该点的坐标.
如图,点(3,m)为直线AB上的点.求该点的坐标. 对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2).
对于平面直角坐标系中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.己知P(1,2),Q(4,2). 小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)
小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)