题目内容
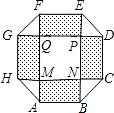 某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.
某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.(1)设矩形的边长AB=x(m),AM=y(m),用含x的代数式来表示y;
(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.
①设该工程的总造价为S(元),求S关于x的函数关系式.
②若该工程的银行贷款为235000元,问仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)根据四个矩形都相同,因此四个直角三角形的直角边都相等,那么可根据4个矩形的面积+中间的正方形的面积=800来列出关于x、y的函数关系式;
(2)①(1)中已得出了矩形的长,那么根据总造价S=4个矩形区域的造价+正方形区域的造价+4个直角三角形区域的造价,来列出关于S、x的函数关系式;
②可将①得出的二次函数式转换成顶点式的表达式,然后看看二次函数的最小值是否超过235000即可.
(2)①(1)中已得出了矩形的长,那么根据总造价S=4个矩形区域的造价+正方形区域的造价+4个直角三角形区域的造价,来列出关于S、x的函数关系式;
②可将①得出的二次函数式转换成顶点式的表达式,然后看看二次函数的最小值是否超过235000即可.
解答:解:(1)y=
(0<x<20
).
(2)①s=2100x2+105×4xy+40×4×
y2
=2100x2+420x×
+80(
-
)2
=2000x2+
+76000(0<x<20
).
②S=2000(x2+
-80)+76000+2000×80=2000×(x-
)2+236000>235000.
所以,光靠银行贷款不能完成该工程的建设任务.
| 800-x2 |
| 4x |
| 2 |
(2)①s=2100x2+105×4xy+40×4×
| 1 |
| 2 |
=2100x2+420x×
| 800-x2 |
| 4x |
| 200 |
| x |
| x |
| 4 |
=2000x2+
| 3 200 000 |
| x2 |
| 2 |
②S=2000(x2+
| 1600 |
| x2 |
| 40 |
| x |
所以,光靠银行贷款不能完成该工程的建设任务.
点评:本题结合实际问题考查了二次函数以及一元二次方程的应用,根据题意找准等量关系从而列出函数关系式是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 已知两个不等式的解集在数轴上如图,那么这个解集为( )
已知两个不等式的解集在数轴上如图,那么这个解集为( )| A、x<-1 | B、x≤2 |
| C、-1<x≤2 | D、x≤-1 |
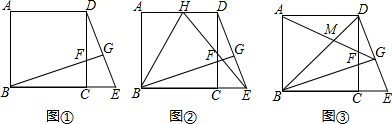
 如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.
如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.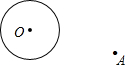 如图,在平面上有一半径为1cm的圆及定点A,OA=4cm.
如图,在平面上有一半径为1cm的圆及定点A,OA=4cm.