题目内容
2. 如图,直线y=ax+b(a、b为常数,且a≠0)与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于点A(-2,4),点B(-4,n),与x轴交于点C;
如图,直线y=ax+b(a、b为常数,且a≠0)与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于点A(-2,4),点B(-4,n),与x轴交于点C;(1)试确定反比例函数的解析式及n的值;
(2)求△AOC的面积.
分析 (1)由A点坐标即可求出反比例函数,再把B点坐标代入反比函数即可求出n的值;
(2)由A、B两点坐标即可求出一次函数的解析式,令y=0代入一次函数中,即可求出C点坐标,过点A作AD⊥x轴于D,所以求出OC、AD的长度即可求出△AOC的面积.
解答 解:(1)把A(-2,4)代入y=$\frac{k}{x}$,
∴k=-8,
∴反比例函数的解析式为y=$\frac{-8}{x}$,
把B(-4,n)代入y=$\frac{-8}{x}$,
∴n=2;
(2)由(1)可知:A(-2,4),B(-4,2),
把A(-2,4),B(-4,2)代入y=ax+b,
∴$\left\{\begin{array}{l}{4=-2a+b}\\{2=-4a+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=6}\end{array}\right.$,
∴一次函数解析式为y=x+6,
把y=0代入y=x+6,
∴x=-6,
∴C(-6,0),
∴OC=6,
过点A作AD⊥x轴于D,
∴AD=4,
∴S△AOC=$\frac{1}{2}$AD•OC=12.
点评 本题考查一次函数综合问题,涉及待定系数求解析式,解方程等知识,综合程度较高,属于中等题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
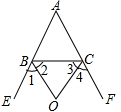 若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC.
若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC. 如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分.
如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分. 如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.
如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.