Question

12．如图，AB为⊙O的直径，C为⊙O上一点，过C点的切线CE垂直于弦AD于点E，连OD交AC于点F．
（1）求证：∠BAC=∠DAC；
（2）若AF：FC=6：5，求sin∠BAC的值．

Answer 1

分析 （1）连结OC，如图1，先利用切线的性质得到OC⊥CD，再判断OC∥AD得到∠CAD=∠ACO，而∠BAC=∠ACO，即可得出结论；
（2）先根据OC∥AD，得出△AFD∽△CFO即可求出$\frac{AD}{OC}=\frac{6}{5}$然后设出AD=6x，OC=5x，再用勾股定理表示出CH，AH，进而得出AC即可求出结论；

解答 （1）证明：连结OC，如图1，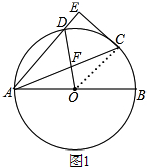

∵CD为切线，
∴OC⊥CD，
∵AD⊥CD
∴OC∥AD，
∴∠CAD=∠ACO，
∵OA=OC，
∴∠BAC=∠ACO，
∴∠BAC=∠DAC，

（2）如图2，

作OG⊥AD于G，CH⊥AB于H，连接OC，
由（1）知，OC∥AD，
∴△AFD∽△CFO，
∴$\frac{AF}{CF}=\frac{AD}{OC}$
∵AF：FC=6：5，
∴$\frac{AD}{OC}=\frac{6}{5}$
设AD=6x，OC=OD=OA=5x，则OG=CH=4x，
在Rt△OCH中，OC=5x，CH=4x，
∴OH=3x，
∴AH=OA+OH=8x；
在Rt△ACH中，AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=4$\sqrt{5}$x
Sin∠BAC=$\frac{CH}{AC}$=$\frac{\sqrt{5}}{5}$．

点评 此题是切线的性质，主要考查了角平分线的判定，切线的性质，相似三角形的判定和性质，勾股定理，锐角三角函数，解本题的关键是求出$\frac{AD}{OC}=\frac{6}{5}$．