题目内容
19.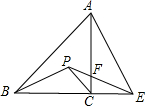 如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.
如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.(1)求证:PB=PE;
(2)试判断线段BC、CE、CP三者之间的数量关系;
(3)若BC=7,当CE=$\sqrt{7}$时,AF=2EF(直接写出结论).
分析 (1)如图1中,连接AP,只要证明△ACP≌△BCP即可.
(2)如图1中,作PD⊥PC交AC于D,则CD=$\sqrt{2}$CP,PD=PC,∠APD=∠EPC,由(1)可知∠CEP=∠CBP=∠CAP,得A、E、C、P四点共圆,再证明△ADP≌△ECP即可解决问题.
(3)如图2中,连接PA,作PH⊥BC于H.设EF=a,PF=b则PA=PE=a+b,AF=2a,先在在RTAPF中利用勾股定理求出a、b的关系,再根据AC=BC=7,列出方程求出a,最后在RT△EFC中利用勾股定理即可解决.
解答 (1)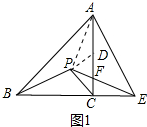 证明:如图1中,连接AP,
证明:如图1中,连接AP,
∵点P在AE的垂直平分线上,
∴PA=PE,
在△ACP和△BCP中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCP}\\{CP=CP}\end{array}\right.$,
∴△ACP≌△BCP,
∴AP=PB=PE.
(2)结论:BC=CE+$\sqrt{2}$CP.
证明:如图1中,由(1)可知∠CEP=∠CBP=∠CAP,
∴A、E、C、P四点共圆,
∴∠APE=∠ACE=90°,作PD⊥PC交AC于D,则CD=$\sqrt{2}$CP,PD=PC,∠APD=∠EPC,
在△ADP和△ECP中,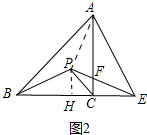
$\left\{\begin{array}{l}{∠PAD=∠PEC}\\{PA=PE}\\{∠APD=∠CPE}\end{array}\right.$,
∴△ADP≌△ECP,
∴AD=CE,
∴BC=AC=AD+CD=CE+$\sqrt{2}$CP.
(3)如图2中,连接PA,作PH⊥BC于H.设EF=a,PF=b则PA=PE=a+b,AF=2a,
在RT△PAF中,∵AF2=PA2+PF2,
∴(2a)2=(a+b)2+b2,
∴b=$\frac{\sqrt{7}-1}{2}$a或b=$\frac{-\sqrt{7}-1}{2}$a(舍弃),
∴PE=$\frac{\sqrt{7}+1}{2}$a=PB ①
∵A、E、C、P四点共圆,
∴AF•CF=EF•PF(相交弦定理),
∴CF=$\frac{EF•PF}{AF}$=$\frac{1}{2}$PF=$\frac{\sqrt{7}-1}{4}$a,
∴CF+AF=7,
$\frac{\sqrt{7}-1}{4}$a+2a=7,
∴a=$\frac{2\sqrt{7}(\sqrt{7}-1)}{3}$,
∴EC=$\sqrt{E{F}^{2}-C{F}^{2}}$=$\sqrt{{a}^{2}-(\frac{\sqrt{7}-1}{4}a)^{2}}$=$\frac{\sqrt{7}+1}{4}$a=$\sqrt{7}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用全等三角形的判定和性质,学会设未知数,用方程的思想解决问题,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
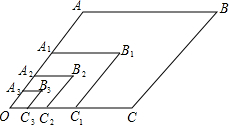 如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032.
如图,在菱形OABC中,∠AOC=60°,OA=2$\sqrt{2}$,以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OABC缩小,得到菱形OA1B1C1;再以点O为位似中心,相似比为$\frac{1}{2}$,将菱形OA1B1C1缩小,得到菱形OA2B2C2;…,以此类推,则菱形OA2016B2016C2016的面积为$\sqrt{6}$×($\frac{1}{2}$)4032. 如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.
如图,已知AB=DC,AC=DB,AC与BD交于一点O,求证:△OBC是等腰三角形.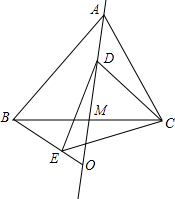 如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.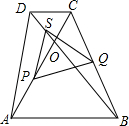 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.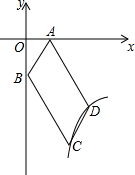 如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
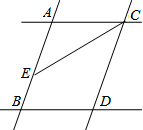 如图,已知AB∥CD,AC∥BD,CE平分∠ACD.
如图,已知AB∥CD,AC∥BD,CE平分∠ACD.