题目内容

11．如图，AB、CD是⊙O的直径，弦CE∥AB，CE为100°，则∠AOC的度数为（　　）
A．30°B．39°C．40°D．45°

分析 由平行弦的性质得出$\widehat{AC}=\widehat{BE}$，求出$\widehat{AC}$的度数，由圆周角定理即可得出结果．

解答 解：∵CE∥AB，
∴$\widehat{AC}=\widehat{BE}$，
∴$\widehat{AC}$的度数=$\frac{1}{2}$（180°-$\widehat{CE}$的度数）=40°，
∴∠AOC=40°；
故选：C．

点评 本题考查了圆周角定理、平行弦的性质；熟练掌握圆周角定理，由平行弦的性质得出相等的弧是解决问题的关键．

练习册系列答案
相关题目
1．如图①，2条直线相交有1个交点，增加1条直线增加2个交点（图②），增加的交点数等于原直线条数2，所以三条直线最多有3个交点；
如图③，再增加1条直线，增加3个交点，增加的交点数等于原直线数3，所以4条直线最多有6个交点．
（1）根据这个规律，请继续把这个表格填完整．
 直线条数 23 4 5 6 7 …
 最多交点数1 3 6 1015 21 …
（2）若有n条直线相交，最多有多少个交点？n=2013时，最多有多少个交点？
2．先化简，再求值：
（1）（3x3y-x2y2+$\frac{1}{2}$x2y）÷（-$\frac{1}{2}$x2y），其中x=-2，y=3；
（2）[（x-y）2+（x+y）•（x-y）]÷2x，其中x=3，y=-1.5．
19．计算：（-$\frac{5}{3}$）a2bc•$\frac{3}{5}$ab2c•（-$\frac{7}{8}$abc2）
6．已知一种药品包装盒如图，其底面是边长分别为8cm和3cm的长方形，侧棱长为6cm，请画出这个直棱柱的表面展开图，并计算这个直棱柱的侧面积和表面积．
16．先化简．再求值：
（$\frac{1}{2}$x+$\frac{1}{3}$y）（$\frac{1}{3}$y-$\frac{1}{2}$x）+$\frac{1}{2}$x（$\frac{1}{2}$x-y），其中x=4，y=6．
3．有一列数：a1=3×2，a2=3×3+1，a3=3×4+2，a4=3×5+3，…，请你研究一下，a8等于什么？并请你用含有n的式子来表示an．（n是正整数）
20．用棋子按下列方式摆图形，设第n个图形所用的棋子数为Sn，依照此规律，第n个图形的棋子数Sn与n的关系式为n（2n-1）．
1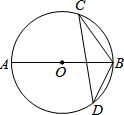．如图，AB是⊙O的直径，C、D是⊙O上的点，若∠ABC=54°，则∠BDC等于（　　）
A．36°B．54°C．72°D．108°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网