Question

8．如图，Rt△ABC的斜边AB与⊙O相切于点B，直角顶点C在⊙O上，若AC=2$\sqrt{2}$，BC=4，则⊙O的半径是（　　）

• A． 3
• B． 2$\sqrt{3}$
• C． 4
• D． 2$\sqrt{6}$

Answer 1

分析 连接BO并延长BO交⊙O于D，连接CD，再结合相似三角形的判定与性质以及勾股定理得出答案．

解答 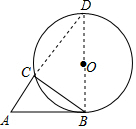解：连接BO并延长BO交⊙O于D，连接CD，
∵BD是⊙O的直径，
∴∠DCB=90°，
又∵∠ACB=90°，
∴点A，C，D在一条直线上，
∵AB切⊙O于D，
∴BD⊥AB，
∵∠A=∠A，
∴△ABD∽△ACB，
∴$\frac{AC}{AB}$=$\frac{AB}{AD}$，
∵Rt△ABC，AC=2$\sqrt{2}$，BC=4，
∴AB=2$\sqrt{6}$，
∴$\frac{2\sqrt{2}}{2\sqrt{6}}$=$\frac{2\sqrt{6}}{AD}$，
解得：AD=6$\sqrt{2}$，
∴DC=6$\sqrt{2}$-2$\sqrt{2}$=4$\sqrt{2}$，
∴BD=$\sqrt{D{C}^{2}+B{C}^{2}}$=4$\sqrt{3}$，
∴⊙O的半径是2$\sqrt{3}$．
故选：B．

点评 此题考查了切线的性质、相似三角形的判定和性质、勾股定理等知识点，作辅助线把半径转化到直角三角形中是关键．