题目内容
18.已知:13=1=$\frac{1}{4}$×1×2213+23=9=$\frac{1}{4}$×22×32
13+23+33=36=$\frac{1}{4}$×32×42
13+23+33+43=100=$\frac{1}{4}$×42×52
…
根据上述规律计算:13+23+33+…+193+203=44100.
分析 观察不难发现,从1开始的连续自然数的立方和等于自然数的个数的平方乘比个数大1的数的平方,再除以4.
解答 解:(1)∵13=$\frac{1}{4}$×12×22,
13+23=$\frac{1}{4}$×22×32,
13+23+33=$\frac{1}{4}$×32×42,
∴13+23+33+…+193+203=$\frac{1}{4}$×202×212=44100;
故答案为:44100.
点评 本题主要考查数字的变化规律,根据题意得出数字的规律是从1开始的连续自然数的立方和等于自然数的个数的平方乘比个数大1的数的平方,再除以4是解题的关键.

练习册系列答案
相关题目
9.在△ABC中,∠C=90°,a+b=14cm,c=10cm,则S△ABC=( )
| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
3.比较-$\frac{1}{2}$与-$\frac{1}{3}$的大小正确的是( )
| A. | -$\frac{1}{2}$<-$\frac{1}{3}$ | B. | -$\frac{1}{2}$>-$\frac{1}{3}$ | C. | -$\frac{1}{2}$=-$\frac{1}{3}$ | D. | -$\frac{1}{2}$≥-$\frac{1}{3}$ |
10.三角形两边长分别为6和5,第三边是方程x2-6x+8=0的解,则这个三角形的周长是( )
| A. | 15或13 | B. | 15 | C. | 15或17 | D. | 13 |
8. 如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
 如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )
如图,Rt△ABC的斜边AB与⊙O相切于点B,直角顶点C在⊙O上,若AC=2$\sqrt{2}$,BC=4,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{6}$ |
 如图,下面几何体由四个大小相同的小立方块组成,则它的左视图是( )
如图,下面几何体由四个大小相同的小立方块组成,则它的左视图是( )



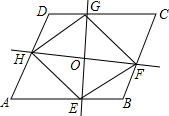 如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.
如图,过?ABCD中对角线的中点O作两条互相垂直的直线,分别交AB、BC、CD、DA于E、F、G、H,试判断四边形EFGH的形状并说明理由.